2-线性表¶

线性表指 0 或 n 个数据元素的有限序列

特点：

元素之间有序
元素个数有限
第一个无直接前驱元素
最后一个无直接后继元素
其余元素都有唯一一个直接前驱元素和唯一一个直接后继元素

线性表元素的个数 \(n(n>=0)\) 即为 线性表的长度；当 n=0 时，称为空表。

非空表中每个数据元素都有一个确定的位置，如\(a_1\)是首个元素，\(a_n\)是最后元素，\(a_i\)是第\(i\)个元素（称 \(i\) 为数据元素 \(a_i\) 在线性表中的位序）

Note

说句人话就是，像数组一样的数据结构就是线性表。

比如拿 5 个苹果排成一行，从左到右依次编号 12345，

第一个苹果前面没有苹果，

最后一个苹果后面没有其他苹果，

中间第 2、3、4 个苹果都有前一个苹果和后一个苹果，

例如第 2 个苹果的前一个苹果是 1 号苹果，后一个是 3 号苹果。

ADT¶

ADT 线性表(List)
Data
    线性表是数据对象集合为{a1, a2, ..., an}，每个元素的类型均为DataType。
Operation
    InitList(*L):          初始化操作，建立一个空的线性表L。
    ListEmpty(L):          线性表为空返回True， 否则返回False
    ClearList(*L):         将线性表清空。
    GetElem(L, i, *e):     将线性表L中第i个位置元素的值返回给e。
    LocateElem(L, e):      在线性表L中查找与给定值e相等的元素，查找成功返回元素在表中的序号，失败返回O。
    ListInsert(*L, i, e):  在线性表L中第i个位置插入新元素e。
    ListDelete(*L, i, *e): 删除线性表L中第i个位置元素，并用e返回其值。
    ListLength(L):         返回线性表L的元素个数。
endADT

顺序结构的线性表¶

线性表的顺序存储结构，指的是用一段连续的存储单元一次存储线性表的数据元素。

例如数组，知道了第一个元素的地址，后面的元素都可以快速的计算出来。

假设第一个元素的 地址为 A，每个元素 占 k 个字节，则可知 第 i 个元素 的地址为 A + i * k。

顺序结构在查找时，不论要查找的元素在任何位置，时间复杂度都为 \(O(1)\)，但在插入和删除时，平均时间复杂度为 \(O(n)\)。

顺序结构代码实现¶

先放上各专业术语的关系图，以做对照。

数据元素¶

各种操作的基本单位是 数据元素，数据元素又由各 数据项 构成。

在代码中，用 结构体类型(C语言中是结构体，Java等语言是类) 来实现数据元素，

用各种 基本类型(int、char、float、其他结构体等) 来实现数据项。（注意数据项也可以是结构体）

// 定义结构体
struct Student{
    char name[10];
    int age;
};

typedef struct Student Stu;    // 为结构体起别名，后续写代码的时候比较方便

或者写成这种：

typedef struct{
    char name[10];
    int age;
}Stu;

在实际应用中数据元素（结构体）名字以实际业务为准

在以下例子中，则用 Element 指代数据元素结构体。

typedef struct{
    char name[10];
    int age;
}Element;

数据对象¶

这里数据对象指的就是线性表了。

线性表中需要包含 N 个数据元素，N 个数据元素要使用数组存放；再加上一个count来统计数据元素个数。

注意是元素个数 (count of data elemment) 不是数组长度(length of array)。

数组长度一开始要预留好，是固定不变的；

元素个数是变化的，增删插入之后都会变化，而数组长度不会。

// DataElement.h

#define len(X) sizeof X / sizeof X[0]
#define MAX_SIZE 5

typedef struct{
    Element elemArr[MAX_SIZE];  // 用数组存放数据元素
    int count;                  // Count of data element.
}SqList;

初始化¶

Status Init(SqList *L, Stu *studArr){
    int length = len(studArr);          // 获取数组长度
    if(length > MAX_SIZE) return ERROR; // 检查数组长度是否超出预设长度

    L->count = 0;   // count 初始化为 0
    for(int i = 0; i < length; i++) 
        Insert(L, i, studArr[i]);   // 调用插入方法将元素插入到数组中（插入方法稍后实现）
    return OK;
}

// main.c

#include "DataElement.h"

int main(){
    // 定义一个线性表
    SqList L;
    SqList *pL = &L;
    // 定义一份数据集
    Stu studArr = {
        {"Boii", 18},
        {"Eva", 20},
    };
    // 初始化线性表
    Init(pL, studArr);
    return 0;
}

获得元素¶

定义
#define OK 1
#define ERROR 0
typedef uint Status;

/**
 * 用pe返回 在线性表L中第position个元素
 * @param *L        要操作是顺序表
 * @param position  要查找的元素位置
 * @param e         负责带回元素的元素指针
 * @return 获得成功返回OK，失败返回ERROR
 */
Status GetElem(SqList *L, int position, Element *e){
    if(L->count == 0 || position < 1 || position > L->count || e == NULL)
        return ERROR;

    *e = L->data[position-1];
    return OK;
}

调用时
SqList L;
SqList *pL = &L;
Element e;
Element *pe = &e;

if(GetElem(pL, 3, pe))
    printf("%s %d", pe->name, pe->age);

函数中先是判断顺序表是否为空表（空表时 count 为 0），接着对位置进行判断，看看是否在合法范围内，还有指针是否为空；

如果满足其中一个条件则返回 ERROR。

最后对将目标元素赋值给 pe。

参数中使用的是 *L，即直接操作目标顺序表

position 代表的是位置，从1开始的（注意不是下标，下标是从0开始的），所以是将 data[position-1] 返回去。

例如查找第5个元素，应该1211。

返回 data[4]

插入¶

/**
 * 将 e 插入到在线性表L中的第 idx 个元素
 * @param *L   要操作是顺序表
 * @param idx  要插入的元素下标
 * @param e    要插入的元素的指针
 * @return 插入成功返回OK，失败返回ERROR
 */
Status Insert(SqList *L, int idx, Element *e){
    // 如果顺序表已满、或下标越界，返回ERROR
    if(L->count == MAX_SIZE || idx < 0 || idx > L->count)
        return ERROR;
    // 如果要插入的位置不在末尾，则从最后一个开始，一个一个往后挪
    if(idx < L->count)
        for(int i = L->count - 1; i >= idx; i--)
            L->data[i + 1] = L->data[i];
    // 将元素插入指定的 idx 
    L->data[idx] = *e;
    L-count++;

    return OK;
}

思路：

表满时，插入失败
下标小于 0 或大于 count - 1 时，插入失败
插入位置在表尾，即 idx = count，直接插入
插入位置不在表尾，即 idx < count，从末尾开始后一位给前一位，直到把 data[idx] 空出来

删除¶

/**
 * 将线性表L中的第 position 个元素删除，被删元素保存在 e 中
 * @param *L        要操作是顺序表
 * @param position  要查找的元素位置
 * @param e         要删除的元素的指针
 * @return 删除成功返回OK，失败返回ERROR
 */
Status Delete(SqList *L, int position, Element *e){
    // 如果空表或者位置超出范围，返回ERROR
    if(L->count == 0 || position < 1 || position > L->count) return ERROR;

    // 将要删除的元素保存起来
    if (e != NULL) *e = L->data[position - 1];

    // 如果删除的不是末尾元素
    if (position < L->count)
        for(int i = position; i < L->count; i++)
            L->data[i - 1] = L->data[i];

    // 元素个数-1
    L->count--;
    return OK;
}

思路：

如果空表，或者位置超出范围[1, count]，删除失败
先将要删除的元素保存起来
如果删除的不是末尾元素，从删除位置开始到顺序表末尾，后一个赋值给前一个，最后元素个数-1
如果删除的是末尾元素，直接元素个数-1

总结¶

数组在查询时，不管元素在哪个位置，时间复杂度都为 O(1)，在删除和插入时，如果位置靠后则挪动的少，如果位置在最前，则整个数组都要挪动。换言之，插入或删除第 i 个元素，需要移动 i - 1个元素。平均移动次数为 (n - 1)/2。所以时间复杂度为O(n)。

顺序结构比较适合元素个数不太变化，而是更多存取数据的应用。

链式结构的线性表¶

线性表的链式结构是指，指的是用不连续的存储单元存储线性表的数据元素。

在链式结构中，除了存储数据元素之外，还要存储其后继元素的地址。

存储数据元素信息的域称为 数据域，存储后继元素地址的域称为 指针域；

这两部分共同组成一个结点，n个结点链结成一个链表，即为线性表的链式存储结构。

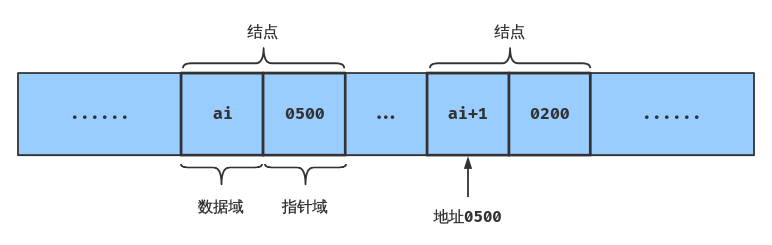
链表的起始结点称为 头结点，头结点中的指针域称为 头指针。

头结点的数据域可以不存储任何信息，也可以存储线性表长度等附加信息；

头结点的指针域指向第一个结点（第一个结点可以称为 首元结点）；

头结点的指针域为空时（即头指针为空时），为空链表。

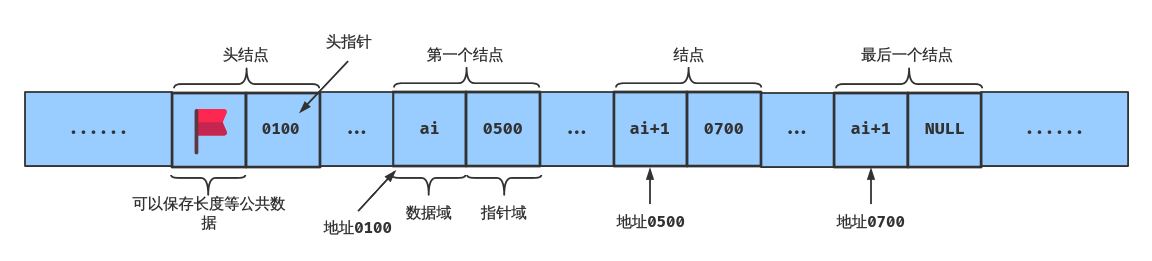
因此，

每个结点只包含一个 后继指针域（指向后继元素的指针域），称为单向链表；

每个结点包含一个 后继指针域（指向后继元素的指针域）和一个 前驱指针域（指向前驱元素的指针域），称为双向链表；

链表的最后一个结点称为 尾结点，尾结点的指针域可以为空（通常用 NULL 或 ^ 表示）

尾结点的 后继指针域 为空时，称为单链表；

尾结点的 后继指针域 指向首元结点的地址时（指向首元结点不是头结点），称为循环链表。

同理，尾结点的 后继指针域 指 \(\to\) 向 首元结点 的地址，首元结点的 前驱指针域 指 \(\to\) 向**尾结点**时，称为双向循环链表。

单链表的代码实现¶

定义结点¶

// 定义数据元素
typedef struct Element {
    char *name;
    int age;
} Element;

// 定义结点
typedef struct Node {
    Element data;           // 数据域
    struct Node* next;      // 指针域，指向本身类型定，称为自引用
} Node;

// 为结点指针定义别名
typedef Node* PNode;

// 定义头结点
typedef struct HeadNode {
    int length;
    struct Node* next;
} HeadNode;

代码中，先是定义了数据元素的结构，然后定义结点。

定义结点的时候，分别定义了数据域和指针域。可以看到指针域其实是自身的指针，这样的实现称为 自引用。

假设 p 是指向第 i 个结点的移动指针，则 p->data 的值第 i 个结点的数据，而 p->next 的值为下一个结点（即第 i + 1个结点）的地址。

用 p = p->next; 可以让移动指针移动到第 i + 1 个结点，这时再使用 p->data 的值就为第 i + 1 个结点的数据。

最后为了方便表示，为这个结点类型的指针定义了一个类型别名 PNode。

PNode p;

创建链表¶

创建链表其实就是创建一个头结点，这个头结点很重要，对链表的操作都是从头结点开始的。

这里形参用的是指针形式，即直接操作该指针。所以在调用 Create() 时取了 link 的地址。

Status Create(HeadNode *head) {
    head->length = 0;
    head->next = null;
    return OK;
}

// 调用时
HeadNode link;
Create(&link);

插入结点¶

插入节点的思路为：

创建新结点并给结点的数据域赋值
如果要插入的位置为 1（即首元节点），则将头结点的 next 给新节点，然后头结点的 next 指向新节点，长度 +1；
如果要插入的位置不为 1，则利用一个 node 指针遍历链表找到要插入位置的前一个结点，将前一个结点的 next 给新节点，然后前一个结点的 next 指向新节点，长度 +1；

Status Insert(HeadNode *head, Element e, int pos) {
    // 如果插入位置超过数组长度，则返回ERROR
    if(pos > head->length) return ERROR;

    // 1. 创建新节点并给新结点的数据域赋值
    Node* newNode = (Node*)malloc(sizeof Node);
    newNode->data = e;
    newNode->next = NULL;

    // 2. 如果插入的位置为首元节点
    if(pos == 1){
        newNode->next = head->next;
        head->next = newNode;
        head->length++;
        return OK;
    }

    // 3. 如果插入的位置不是首元节点
    //    声明一个移动指针遍历遍历直到达到要插入的位置的前一个结点
    //    因为要到达前一个结点，所以这里走到 pos - 1 即可
    Node* p = head->next;
    for(int i = 1; p && i < pos - 1; i++){
        p = p->next;
    }
    newNode->next = p->next;
    p->next = newNode;
    head->length++;
    return OK;
}

// 调用时
Element e = {"Boii", 18};
Insert(&head, e, 4);

Note

链表插入的重点在于要先将 前一个结点的指针域新节点的指针域 newNode->next = p->next ，然后再把 新节点的地址给前一个结点的指针域 p->next = newNode ，这两者顺序不能颠倒，否则会插入失败。

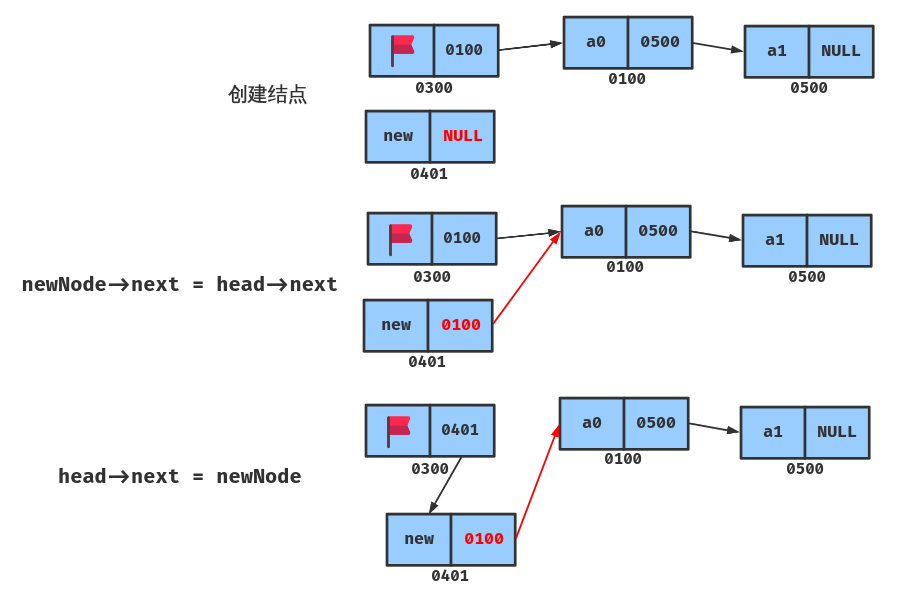
初始化链表¶

初始化链表时需要将 头结点 和 元素数组 传给函数

上面我们已经定义好了创建链表函数，插入结点函数，所以在初始化时非常方便，只需要调用Create()创建链表，然后遍历元素数组，调用Insert()即可。

Status Init(HeadNode *head, Element *datas){
    // 创建链表
    if(Create(head)){
        // 遍历元素数组
        for(int i = 0; i < (sizeof datas / sizeof datas[0]); i++)
            Insert(head, datas[i], i + 1);
        return OK;
    }
    return ERROR;
}

// 调用时
Element datas = {
    {"Alice", 18},
    {"Boii", 20},
    {"Candy", 22}
};

HeadNode head;
Init(&head, datas);

读取结点¶

假设现在要读取第 i 个结点，在读取结点之前，要先找到结点，然后把数据保存起来。

获得链表第 i 个数据的思路：

声明一个移动指针 p，让 p 指向第一个结点；
声明一个计数器 j，初始化 j 从 1 开始（因为 j 是用来和 i 做比较的，i 是从1开始算的）；
当 j < i 时，就遍历链表，一直让移动指针 p 向后移动并且 j++，直到 j == i；
若到链表末尾 p 为空，则说明没找到第 i 个数据；
否则查找成功，返回 p 指向的结点的数据。

Status GetElem(PNode List, int i, Element *e) {
    PNode p = List->next;   // 指向头结点；
    int j = 1;              // 初始化计数器

    while(j < i || p ) {
        p = p->next;    // 让移动指针指向下一个结点
        j++;
    }

    // 如果 p 为空 或者 j > i, 说明没找到，返回 error
    if(!p || j > i) return ERROR;

    *e = p->data;
    return OK;
}

删除结点¶

删除思路：

创建一个结点指针 Node*来暂存要被删除的结点的地址
找到要被删除的结点的前一个结点
让前一个结点的 next 指向被删结点的下一个结点
free 释放被删结点的内存

Status Delete(HeadNode *head, int pos){
    if(pos > head->length)
        return ERROR;

    Node* p = head->next;
    /* 1. 如果删除的是首元节点 */
    if(pos == 1){
        head->next = p->next;
        head->length--;
        free(p);
        return OK;
    }
    /* 2. 如果删除的不是首元结点 */
    /* 先找到要删除结点的前一个结点 */
    for(int i = 1; p && i < pos - 1; i++){
        p = p->next;
    }
    /* 然后删除目标结点 */
    Node *q = p->next;          // 创建一个Node型指针暂存被删结点
    p->next = q->next;          // 让被删结点的前驱元素的 next 指向被删结点的后驱元素
    head->length--;             // 长度-1

    free(q);                    // 释放被删结点的空间
    q = p = NULL;               // 指针置空
    return OK;
}

Note

C语言需要自己管理内存，自己管理指针释放指针，所以在删除之前要先将被删除结点保存起来，改链（p->next = q->next）之后将被删除结点的内存释放，最后把函数里创建的指针置空。

删除 i 结点其实就是让 i - 1 结点指向 i + 1.

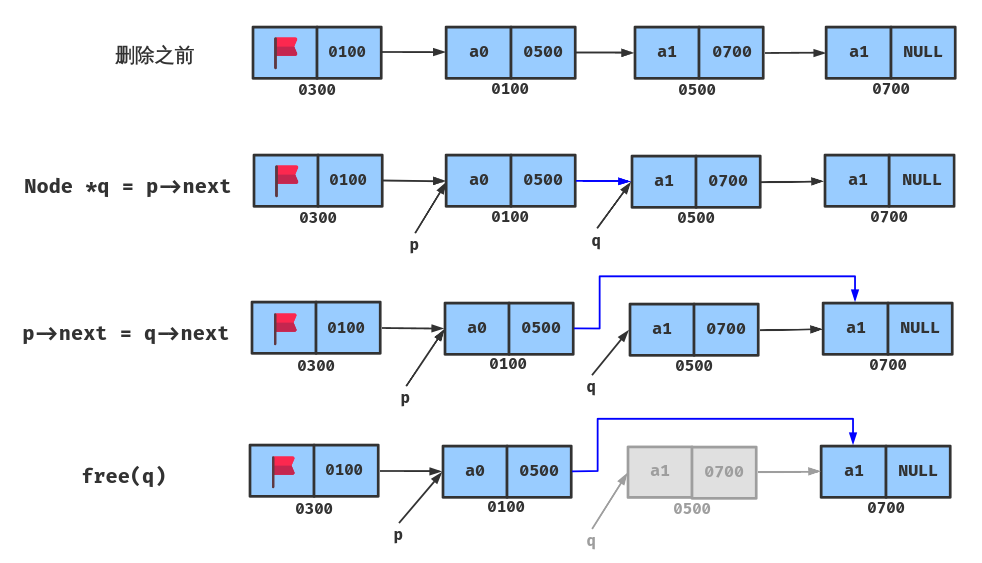
循环链表¶

循环链表与单链表相比多了一个 尾元结点指向首元节点。可以把尾元结点的指针称为 尾指针。

当遍历循环链表时，可以通过判断 尾元结点->next == 头结点->next得知是否遍历了一圈了。

其实循环链表可以有2种实现形式：

尾指针指向头结点
尾指针指向首元结点

可根据需要选择相应的设计。

在操作上，循环链表和单链表的区别主要在插入和删除上。

插入操作¶

循环链表的插入操作要考虑4种情况

链表是否为空
插入位置为首元节点
插入位置为尾元结点
插入位置为中间结点

Status Insert(HeadNode *head, Element e, int pos){

    if(pos > head->length) return ERROR;

    // 创建新结点
    Node *newNode = (Node*)malloc(sizeof Node);
    newNode->data = e;
    newNode->next = NULL;

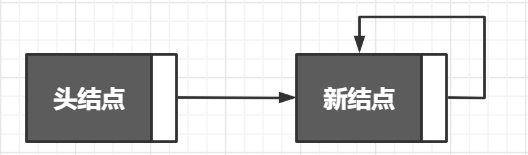
    /** 1. 链表为空 */
    if(!head->length){
        newNode->next = newNode;    // 让新结点的后继指针指向自己
        head->next = newNode;       // 让头结点指向新结点
        head->length++;
        return OK;
    }

    /** 链表不为空 */
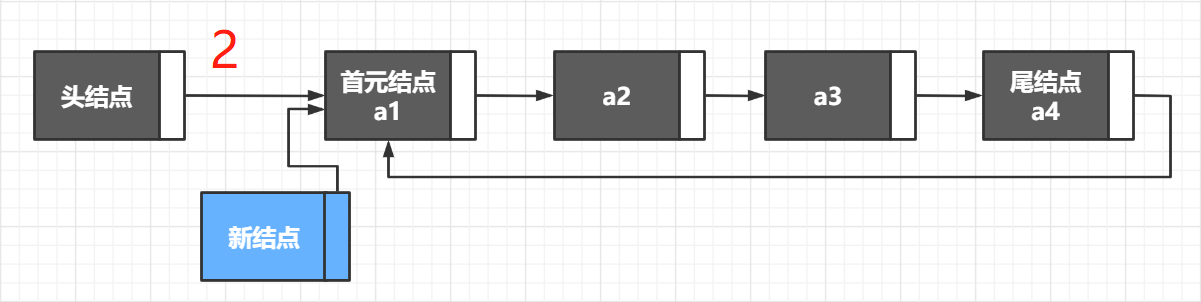
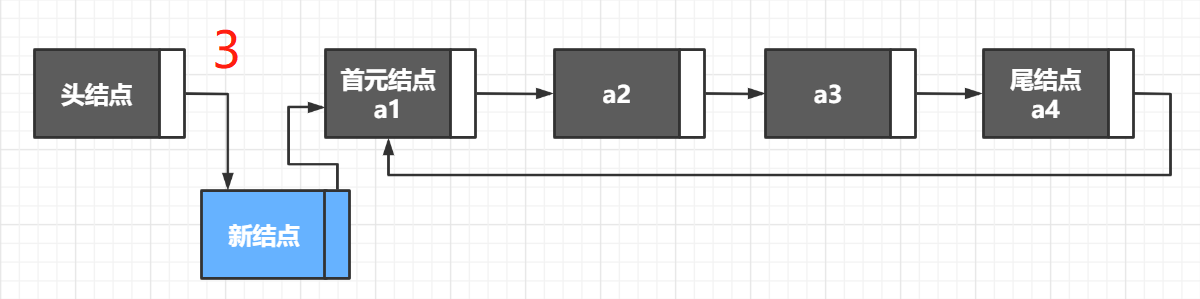
    /** 2. 插入位置为首元结点 */
    if(pos == 1){
        // 先把新结点做插入操作
        newNode->next = head->next;
        head->next = newNode;
        head->length++;
        // 找到尾结点
        Node *last = head->next;
        for(int i = 0; i < head->length; i++) last = last->next;
        // 让尾指针指向新结点
        last->next = newNode;
        return OK;
    }

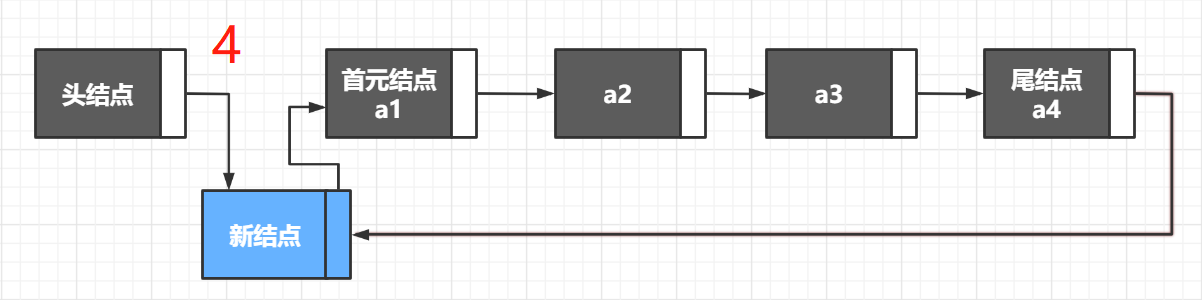
    /** 3. 插入位置为尾元结点 */
    if(pos == head->length){
        // 找到尾结点
        Node *last = head->next;
        for(int i = 0; i < head->length; i++) last = last->next;
        // 让新结点指向头结点，让尾结点指向新结点
        newNode->next = head->next;
        last->next = newNode;
        head->length++;

        return OK;
    }

    /** 4. 插入位置为中间结点*/
    if(pos != head->length){
        // 找到目标位置的前一个
        Node *p = head->next;
        for(int i = 1; p && i < pos - 1; i++) p = p->next;
        // 做普通插入操作
        newNode->next = p->next;
        p->next = newNode;
        head->length++;

        return OK;
    }    
}

当链表为空时，插入新结点只需要让新结点指向自己，然后让头结点指向新结点即可
当链表不为空
- 插入位置为首元结点时，先做一个普通的插入操作，然后找到尾结点让尾指针指向新结点即可
- 插入位置为尾元结点时，找到尾元结点，让新结点指向头结点，让尾指针指向新结点即可
- 插入位置为中间结点时，找到目标位置前一个结点，做一个普通插入操作即可

循环链表删除操作¶

Status DeteleCLinkList(HeadNode* head, int pos)
{
    // 判断位置是否正确，或是否为空链表
    if (isEmptyC(head) || pos > head->length)
        return ERROR;

    // 如果是删除首元结点
    if (pos == 1) {
        Node* first = head->next;
        head->next = first->next;

        Node* last = GetLast(head);
        last->next->next = head->next;

        head->length--;
        free(first);
        return OK;
    }

    // 如果是删除尾元结点
    if (pos == head->length) {
        Node* last = GetLast(head);
        last->next = head->next;

        head->length--;
        free(last);
        return OK;
    }
    // 1、找到目标结点
    Node* current = head->next;
    for (int i = 1; i < pos - 1; i++) {
        current = current->next;
    }
    // 2、进行删除操作
    Node* q = current->next;
    current->next = q->next;
    head->length--;
    free(q);
    return OK;
}


/** 返回尾结点的前驱结点 */
Node* GetLast(HeadNode* head)
{
    if (!head->length) {
        printf("链表为空！");
    }
    if (head->length == 1) {
        return head->next;
    }

    Node* last = head->next;
    for (int i = 0; i < head->length - 1; i++) {
        last = last->next;
    }
    return last;
}