3-栈
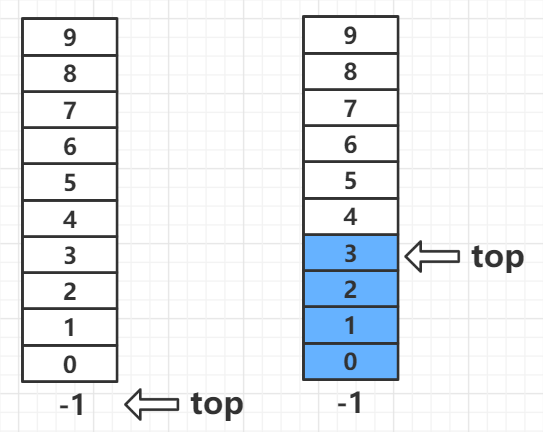
栈是一种只允许在一端进行插入和删除操作的操作受限的线性表。
栈的主要特点是 先进后出 (FILO),就像子弹夹一样,最先压进去的子弹最后打出来。
栈有一个指针,永远指向栈的最顶部,称作 栈顶指针。
栈的另外一个概念是 栈底指针,在顺序栈中可不实现,在链栈中必须实现。
对于栈的操作有插入和删除,也称作 入栈 和 出栈,不能从中间取出,因为只有一个口。
栈的主要操作包括:创建、初始化、入栈、出栈、判空、判满、获取栈顶元素、清空栈。
栈的应用非常广,例如函数调用就是用栈实现的。栈这种前进后出的特点非常适合解决匹配问题。
顺序栈
定义
| #ifndef DATAELEMENT_H_INCLUDED
#define DATAELEMENT_H_INCLUDED
#define MAX_SIZE 10
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Bool;
typedef int Status;
/** 数据元素 */
typedef struct {
int id;
char* name;
} Element;
/** 栈 */
typedef struct {
Element datas[MAX_SIZE];
int top; // 栈顶指针
} Stack;
#endif // DATAELEMENT_H_INCLUDED
|
创建
| Status Create(Stack *s) {
s->top = -1;
return OK;
}
|
栈空条件有两种:s->top == -1、s->top == 0
这里采用 -1 这种,原因是不需要浪费一个元素大小的空间,另外操作起来也方便,因为数组下标是从0开始的。
初始化
| Status Init(Stack* s, Element* datas, int length) {
if (length > MAX_SIZE)
return ERROR;
if (s->top != -1)
Create(s);
for (int i = 0; i < length; i++)
push(s, datas[i]);
return OK;
}
|
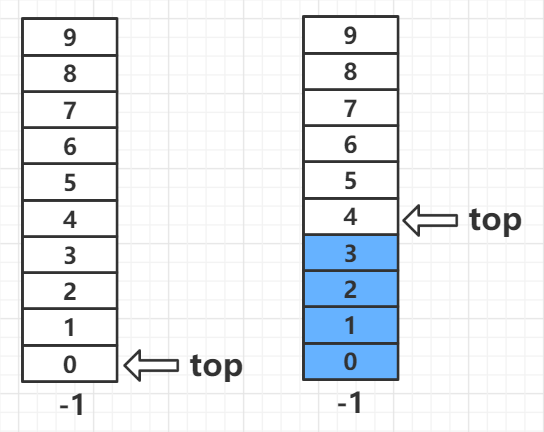
入栈
| Status push(Stack* s, Element e) {
if (s->top >= MAX_SIZE - 1)
return ERROR;
s->datas[++s->top] = e;
return OK;
}
|
我们采用的是第一种栈空表示方式,栈顶指针永远指向栈顶元素,所以在将元素赋值压入栈之前,要先把栈顶指针抬起来 1 格,然后再把元素放进去。
s->datas[++s->top] = e 等价于
| s->top++;
s->datas[s->top] = e
|
出栈
| Element pop(Stack* s) {
return s->datas[s->top--];
}
|
出栈的道理相同,先把元素取出来,然后栈顶指针降下去1格。
s->datas[s->top--] 等价于
| s->datas[s->top];
s->top--;
|
获取栈顶元素
获取栈顶元素不会出栈,就像把弹夹取下来看一眼,并不是打出去。
| Element get(Stack* s) {
return s->datas[s->top];
}
|
判空
我们采用的是第一种栈空表示方式,所以只要判断栈顶指针是不是 s->top == -1 21即可。
| Bool isEmpty(Stack* s) {
return s->top == -1;
}
|
判满
| Bool isFull(Stack* s) {
return s->top == MAX_SIZE - 1 ? TRUE : FALSE;
}
|
清空栈
| Status Clean(Stack* s) {
s->top = -1;
return OK;
}
|
顺序栈的清空很简单,只需要把栈顶指针指向栈底即可,虽然原本的数据没有被销毁,但是后续push的数据会将其覆盖。即使没有覆盖,在栈中我们只需要关注栈顶指针 top 的指向即可,top 所指即为栈顶,不论 top 之上有没有数据。
至于销毁栈,需要在定义 Stack s 的地方 free(s) 。
打印栈
| void Show(Stack* s) {
for (int i = 0; i <= s->top; i++)
printf("%d \t %s \n", s->datas[i].id, s->datas[i].name);
}
|
测试数据
| #include "SqStack.c"
Element datas[] = {
{ 1, "Iron Man" },
{ 2, "Green Man" },
{ 3, "Thor" },
{ 4, "Doctor" }
};
int main()
{
Stack s;
Create(&s);
Init(&s, datas, sizeof datas / sizeof datas[0]);
Show(&s);
printf("\n----------------------------------\n");
Element e = { 5, "Big Man" };
push(&s, e);
Show(&s);
printf("\n----------------------------------\n");
Element pe = pop(&s);
pop(&s);
Show(&s);
return 0;
}
// ---------------------------------------------------
// Output:
1 Iron Man
2 Green Man
3 Thor
4 Doctor
----------------------------------
1 Iron Man
2 Green Man
3 Thor
4 Doctor
5 Big Man
----------------------------------
1 Iron Man
2 Green Man
3 Thor
|
链栈
定义
| #ifndef DATAELEMENT_H_INCLUDED
#define DATAELEMENT_H_INCLUDED
#define MAX_SIZE 10
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
typedef int Bool;
/** 数据元素 */
typedef struct {
int id;
char* name;
} Element;
/** 链栈结点 */
typedef struct Node {
Element data;
struct Node* next;
} Node;
/** 链栈 */
typedef struct {
Node* next;
int top;
} LStack;
#endif // DATAELEMENT_H_INCLUDED
|
链栈稍微比顺序栈复杂一点点,但是换来不限栈大小的好处,所以在链栈中没有栈满的概念。
同时,链栈在入栈的时候需要手动分配空间,在出栈的时候需要把结点中的数据保存起来,销毁结点,再把数据返回。
创建
| Status Create(LStack* s) {
s->next = NULL;
s->top = -1;
return OK;
}
|
初始化
| Status Init(LStack* s, Element* datas, int length) {
if (s->top != -1)
Create(s);
for (int i = 0; i < length; i++)
push(s, datas[i]);
return OK;
}
|
入栈
| Status push(LStack* s, Element e) {
// 建立新结点,分配空间
Node* new = (Node*)malloc(sizeof(Node));
// 判断分配空间是否成功
if (!new)
return ERROR;
new->data = e;
// 插入到链表的首元结点,成为栈顶元素
new->next = s->next;
s->next = new;
s->top++;
}
|
这里的入栈使用的是头插法,即每个新插入的元素都会插在链表的首元结点的位置。
出栈
| Element pop(LStack* s) {
Element res;
if (isEmpty(s)) {
return res;
}
Element res = s->next->data; // 将栈顶元素的数据复制一份
// 改链,原本指向栈顶元素,现在指向栈顶的下一个元素,使其成为新的栈顶
Node* p = s->next;
s->next = p->next;
// 将旧的栈顶元素释放空间
free(p);
s->top--;
return res;
}
|
链栈的出栈操作要记得把被弹出栈的旧栈顶元素释放。
获取栈顶元素
| Element get(LStack* s) {
return s->next->data;
}
|
判空
| Bool isEmpty(LStack* s) {
return s->top == -1;
}
|
清空栈
| Status Clean(LStack* s)
{
if (s->top == -1) {
return OK;
}
Node* deleted = s->next;
Node* p;
while (deleted) {
p = deleted->next;
free(deleted);
deleted = p;
}
// s->next = NULL;
// s->top = -1;
Create(s);
return OK;
}
|
清空链栈和销毁链表的操作是相同的,需要定义两个结点指针,相互配合实现整表销毁。
最后将栈置空,栈顶指针恢复到初试状态,所以这里调用了 Create(),等价于其上面两句表达式。
打印链栈
| void Show(LStack* s) {
if (s->top == -1) {
printf("Stack is EMPTY!");
return;
}
Node* p = s->next;
for (int i = s->top; i > -1; i--) {
printf("%d \t %s \n", p->data.id, p->data.name);
p = p->next;
}
}
|
测试数据
| #include "LinkStack.c"
Element datas[] = {
{ 1, "Iron Man" },
{ 2, "Green Man" },
{ 3, "Thor" },
{ 4, "Doctor" }
};
int main()
{
LStack s;
Init(&s, datas, 4);
Show(&s);
printf("\n----------------------------------\n");
Element e = { 5, "Big Man" };
push(&s, e);
Show(&s);
printf("\n----------------------------------\n");
Element pe = pop(&s);
pop(&s);
Show(&s);
printf("\n----------------------------------\n");
Clean(&s);
Show(&s);
return 0;
}
// ---------------------------------------------------
// Output:
4 Doctor
3 Thor
2 Green Man
1 Iron Man
----------------------------------
5 Big Man
4 Doctor
3 Thor
2 Green Man
1 Iron Man
----------------------------------
3 Thor
2 Green Man
1 Iron Man
----------------------------------
Stack is EMPTY!
|
共享栈
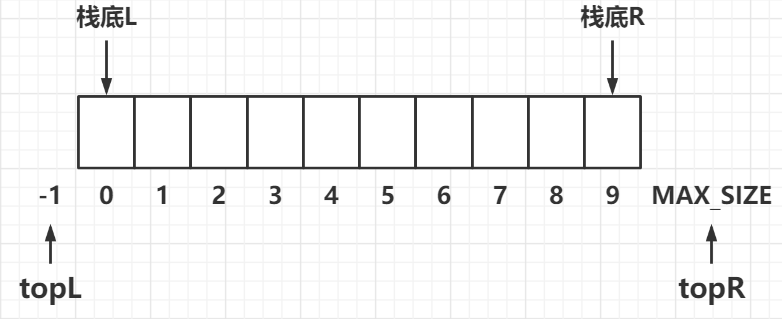
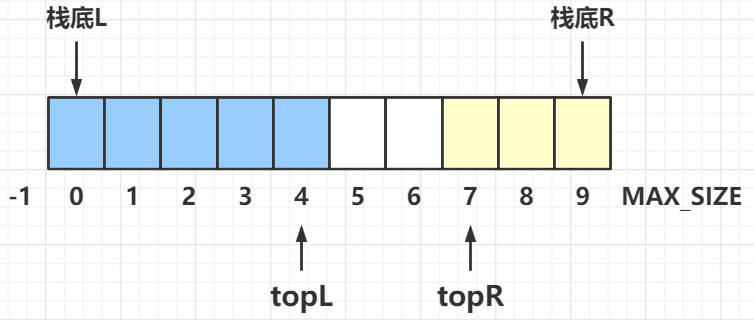
共享栈:指的是两个栈共用一个内存空间的一种栈结构。
共享栈不需要用链式结构,因为共享栈为的是 节省空间,用链式没有意义。
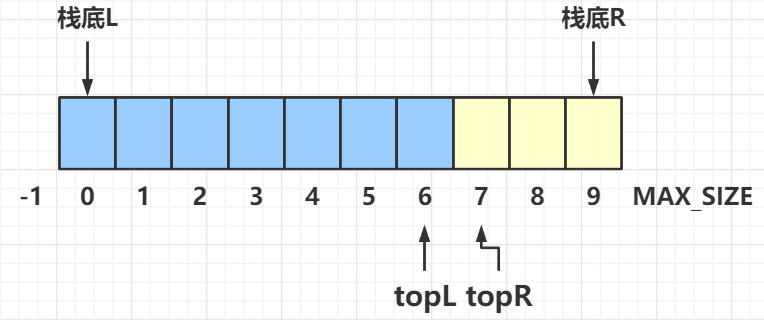
两个栈的栈底固定不变,讲两个栈顶设置在数组的两端,即 左边的栈 s0 的栈底设在 0 处,右边的栈 s1 的栈底设在 MAX_SIZE - 1 处。
创建共享栈时,左栈的栈顶指针 topL = -1,右栈的栈顶指针 topR = MAX_SIZE,当两个栈顶相遇时栈满,这样可以尽可能地利用空间。
定义
共享栈的定义稍稍不同。
| #ifndef DATAELEMENT_H_INCLUDED
#define DATAELEMENT_H_INCLUDED
#define MAX_SIZE 10
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define LEFT 1 // 和顺序栈的定义相比多一个 LEFT 和 RIGHT 来标记方向
#define RIGHT 999
typedef int Bool;
typedef int Status;
typedef struct {
int id;
char* name;
} Element;
typedef struct {
Element datas[MAX_SIZE]; // 栈的存储空间,用数组来存储
int topL; // 左栈的栈顶指针
int topR; // 右栈的栈顶指针
} ShareStack;
#endif // DATAELEMENT_H_INCLUDED
|
创建
| Status Create(ShareStack* s)
{
s->topL = -1;
s->topR = MAX_SIZE;
return OK;
}
|
初始化
| Status Init(ShareStack* s, Element* datas, int length, int direction)
{
if (length > MAX_SIZE) {
return ERROR;
}
if (direction == LEFT && !isEmptyL(s)) {
s->topL == -1;
}
if (direction == RIGHT && !isEmptyR(s)) {
s->topR = MAX_SIZE;
}
for (int i = 0; i < length; i++) {
push(s, datas[i], direction);
}
return OK;
}
|
共享栈需要多一个参数 direction,来指定将元素放入左栈还是右栈。
入栈
| Status push(ShareStack* s, Element e, int direction)
{
if (isFull(s)) {
return ERROR;
}
switch (direction) {
case LEFT:
s->datas[++s->topL] = e;
return OK;
case RIGHT:
s->datas[--s->topR] = e;
return OK;
default:
printf("Direction is ILLEGAL PARAMETER!");
return ERROR;
}
}
|
出栈
| Element pop(ShareStack* s, int direction)
{
Element e;
switch (direction) {
case LEFT:
if (isEmptyL(s)) {
return e;
}
e = s->datas[s->topL--];
return e;
case RIGHT:
if (isEmptyR(s)) {
return e;
}
e = s->datas[s->topR--];
return e;
default:
printf("Direction is ILLEGAL PARAMETER!");
break;
}
}
|
获取栈顶元素
| Element get(ShareStack* s, int direction)
{
return s->datas[direction == LEFT ? s->topL : s->topR];
}
|
判空
| Bool isEmpty(ShareStack* s)
{
return s->topL == -1 && s->topR == MAX_SIZE;
}
Bool isEmptyL(ShareStack* s)
{
return s->topL == -1;
}
Bool isEmptyR(ShareStack* s)
{
return s->topR == MAX_SIZE;
}
|
判满
| Bool isFull(ShareStack* s)
{
return s->topL == s->topR - 1;
}
|
清空栈
| Status Clean(ShareStack* s, int direction)
{
if (isEmpty(s)) {
return OK;
}
switch (direction) {
case LEFT:
s->topL = -1;
break;
case RIGHT:
s->topR = MAX_SIZE;
break;
default:
return ERROR;
}
return OK;
}
|
打印栈
| void Show(ShareStack* s, int direction)
{
if (isEmpty(s)) {
printf("The Whole Share stack is EMPTY!\n");
}
switch (direction) {
// 打印左栈
case LEFT:
if (isEmptyL(s)) {
printf("The Left Share stack is EMPTY!\n");
return;
}
for (int i = 0, j = 1; i <= s->topL; i++, j++) {
printf("No. %d is: %d \t %s \n", j, s->datas[i].id, s->datas[i].name);
}
break;
// 打印右栈
case RIGHT:
if (isEmptyR(s)) {
printf("The Right Share stack is EMPTY!\n");
return;
}
for (int i = s->topR, j = 1; i < MAX_SIZE; i++, j++) {
printf("No. %d is: %d \t %s \n", j, s->datas[i].id, s->datas[i].name);
}
break;
// 如果传进来的不是 LEFT 也不是 RIGHT,则打印整个栈
default:
for (int i = 0; i < MAX_SIZE; i++) {
if (i > s->topL && i < s->topR) { // 超过左栈没到右栈的这段空白
printf("No. %d is EMPTY.\n", i + 1);
} else {
printf("No. %d is: %d \t %s \n", i + 1, s->datas[i].id, s->datas[i].name);
}
}
break;
}
}
|
测试数据
| #include "ShareStack.c"
#define len(X) sizeof(X) / sizeof(X[0])
Element datas1[] = {
{ 1, "Iron Man" },
{ 2, "Green Man" },
{ 3, "Thor" },
{ 4, "Doctor" }
};
Element datas2[] = {
{ 12, "Spider Man" },
{ 24, "Wonder Woman" },
{ 35, "Bat Man" },
{ 40, "Super Man" }
};
int main()
{
ShareStack ss;
Create(&ss);
Init(&ss, datas2, len(datas2), RIGHT);
Show(&ss, RIGHT);
printf("\n----------------------------------\n");
Init(&ss, datas1, len(datas1), LEFT);
Show(&ss, LEFT);
printf("\n----------------------------------\n");
Show(&ss, 10);
return 0;
}
// ---------------------------------------------------
// Output:
No. 1 is: 40 Super Man
No. 2 is: 35 Bat Man
No. 3 is: 24 Wonder Woman
No. 4 is: 12 Spider Man
----------------------------------
No. 1 is: 1 Iron Man
No. 2 is: 2 Green Man
No. 3 is: 3 Thor
No. 4 is: 4 Doctor
----------------------------------
No. 1 is: 1 Iron Man
No. 2 is: 2 Green Man
No. 3 is: 3 Thor
No. 4 is: 4 Doctor
No. 5 is EMPTY.
No. 6 is EMPTY.
No. 7 is: 40 Super Man
No. 8 is: 35 Bat Man
No. 9 is: 24 Wonder Woman
No. 10 is: 12 Spider Man
|