6-树¶

前面的线性表、广义表、栈、队、串，都是一对一的数据结构。

现在开始我们要讨论一种一对多的数据结构: 树。

定义¶

树是 n 个结点的有限集。

n=0 时称为空树。

n>1 时，有且仅有一个特定的根节点 root，其余结点可分为 m（m>0）个互不相交的有限集 \(T_1、T_2、...、T_m\)，其中每个集合本身又是一棵树，称为子树。

名词解释¶

名词	解释	示例
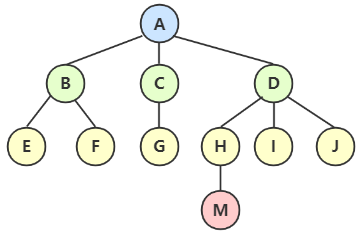
结点	树中的一个独立单元。包含一个数据元素及若干指向其他子树的分支。	eg：图中每一个圆圈都是结点。
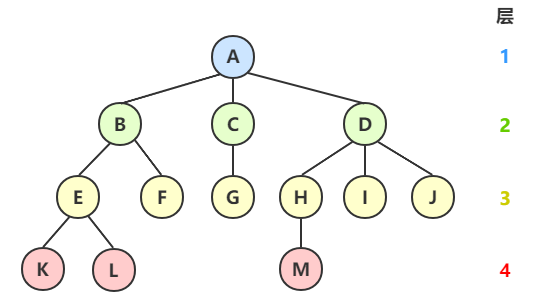
结点的度	结点拥有的子树的数量。	eg：A的度为3，B的度为2，C的度为1。
树的度	树内各结点的度的最大值。	eg：上面的树的度为3。
树的高度（深度）	树中的最大层数。	eg：图中树的深度（高度）为 4。
叶子结点	度为0的结点，也称终端结点。	eg：K、L、F、G、M、I、J 都是叶子结点。
分支结点	度不为0的结点，也称非终端结点。	eg： A、B、C、D、E、H 都是非终端结点。
双亲结点	一个结点的直接前驱结点称为其双亲结点。	eg：E的双亲为B，G的双亲为C。
孩子结点	一个结点的所有直接后继结点称为其孩子结点。	eg：B的子结点为E、F，H的子结点为M。
兄弟结点	同一个双亲的子结点之间互称兄弟结点。	eg：H的兄弟结点为I、J。
祖先	从一个结点到根节点所经分支上的所有结点。	eg：K的祖先为E、B、A。
子孙	一个结点所有直接和间接后继结点。	eg：D的子孙为H、I、J、M。
堂兄弟	双亲在同一层的结点互为堂兄弟。	eg：G与E、F、H、I、J 互为堂兄弟。
层	根为第一层，根的孩子为第二层，以此类推	eg：A为1层，B、C、D为2层，K、L、M为3层。

有序树、无序树：树中的结点从左至右依次有序不能互换，称为有序，否则称为无序。有序树中最左边的子树称为根节点的第一个孩子，最右边称为根节点的最后一个孩子。

森林：m 棵不相交的树的集合。

ADT¶

ADT Tree
Data
    树是由一个根结点和若干子树构成。树中结点具有相同数据类型及层次关系。
Operation
    InitTree(T*): 构造空树T
    DestoryTree(T*): 销毁树T
    CreateTree(T*, definition): 按definition中给出的树的定义来构造树
    ClearTree(T*): 若树T存在，则将树T清空为空树
    TreeEmpty(T): 若T为控诉，返回true，否则返回false
    TreeDepth(T): 返回树T的深度
    Root(T): 返回T的根节点
    Value(T, cur_e): cur_e 是树T中一个结点，返回此结点的值
    Assign(T, cur_e, value): 给树T的结点cur_e赋值为 value
    Parent(T, cur_e): 若 cur_e 是树T的非根结点，则返回它的双亲，否则返回空
    LeftChild(T, cur_e): 若 cur_e 是树T的非叶结点，则返回它的最左孩子，否则返回空
    RightSibling(T, cur_e): 若 cur_e 有右兄弟，则返回它的右兄弟，否则返回空
    InsertChild(T*, p*, i, c): 其中p指向树T的某个结点，i为所指结点p的度+1，非空树c与T不相交，操作结果为插入c为树T中p指结点的第i棵子树
    DeleteChild(T*, p*, i): 其中p指向树T的某个结点，i为所指结点p的度，操作结果为删除T中p所指结点的第i棵子树
endADT

存储结构¶

顺序结构¶

双亲表示法¶

除了根节点，其他结点一定有双亲结点

双亲表示法有两种：

只能简单的记录结点关系的一维数组
带数据域和指示域的多维数组

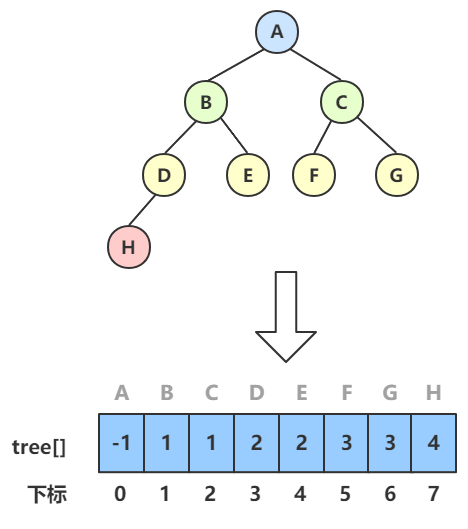
我们利用 一维数组，下标表示树中的结点，数组元素的内容表示该结点的双亲结点。

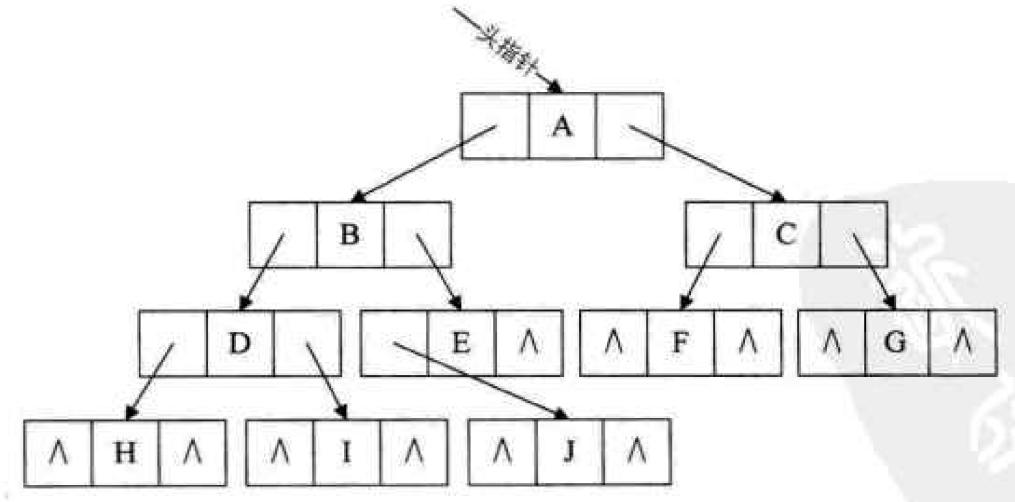
用 结构数组，每个结点附设一个指示器指示其双亲结点在表中的位置。上图的树用多维数组表示为：

下标	数据	双亲
0	A	-1
1	B	0
2	C	0
3	D	1
4	E	1
5	F	2
6	G	2
7	H	3

用代码实现如下：

#define MAX_TREE_SIZE 100

typedef char Element;    // 数据元素类型，暂定为字符型

typedef struct {
    Element data;    // 数据域
    int parent;      // 双亲位置
} PTNode;

typedef struct {
    PTNode nodes[MAX_TREE_SIZE];    // 结点数组
    int root, node_count;    // 根的位置和结点数
} PTree;

Status insert(PTree* pt, Element e, int p) {
    pt->nodes[pt->node_count].data = e;
    pt->nodes[pt->node_count].parent = p;
    if (p == -1) pt->root = pt->node_count;
    pt->node_count++;
}

这种结构的话很容易找到一个结点的双亲结点，如果parent为-1即表示此结点为根节点。

但是如果要找结点的孩子，只能遍历整个数组。

链式结构¶

二叉树 Binary Tree¶

定义¶

二叉树是 n（n >= 0）个结点的有限集合，该集合或者为空集，或者有一个根结点和两棵不相交的分别称为根结点的左子树和右子树的二叉树组成。

一棵树的度为 n 时，又称 n 叉树。所以二叉树的度为2，即每个结点最多有2个子结点。

特点¶

每个结点最多有两棵子树，所以二叉树中不存在度 > 2 的结点。
左子树和右子树是有顺序的，次序不能任意颠倒。就像左手是左手，右手是右手，不能互换。
即使树中某结点只有一棵子树，也要区分是左子树还是右子树。就像摔伤了左手还是右手，对你生活的影响程度是不一样的。

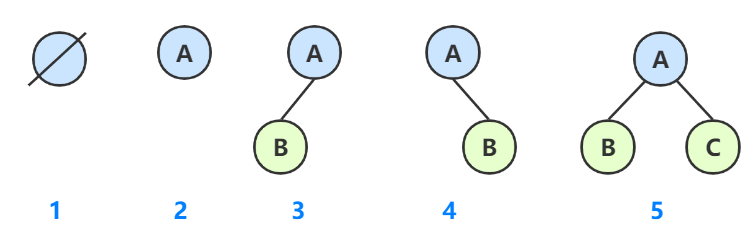
二叉树有5种基本形态：

空二叉树
只有根节点
根节点+左子树
根节点+右子树
根节点+左子树+右子树

斜树¶

所有结点都只有左子树的二叉树叫左斜树

所有结点都只有右子树的二叉树叫右斜树

斜树有很明显的特点，每一层都只有一个结点，结点的个数与二叉树的深度相同。

满二叉树¶

满二叉树

在一棵二叉树中，所有分支节点都有左子树和右子树，且所有叶结点都在同一层，则称为满二叉树。

注意单是每个结点都存在左右子树还不够，那样只算完全二叉树，还需要叶子节点都在同一层。

满二叉树的特点有：

叶结点只能出现在最下层，其他层出现就不可能达成平衡
分支结点的度必须 = 2，否则就是缺胳膊少腿了。
在同样深度的二叉树中，满二叉树的结点树最多，叶子最多。

完全二叉树¶

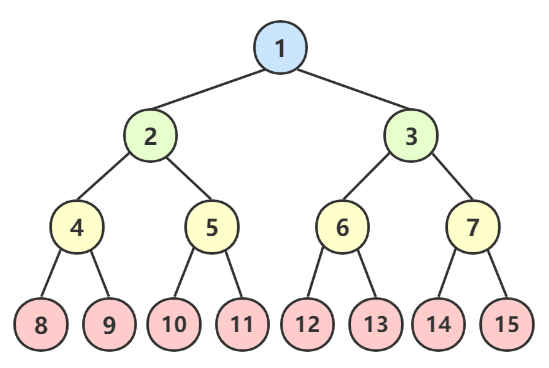
对一棵具有 n 个结点的二叉树按层序编号，如果编号为 i（1 <= i <= n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

一棵满二叉树一定是完全二叉树，一棵完全二叉树不一定是满二叉树。

注意完全二叉树是 按层序编号

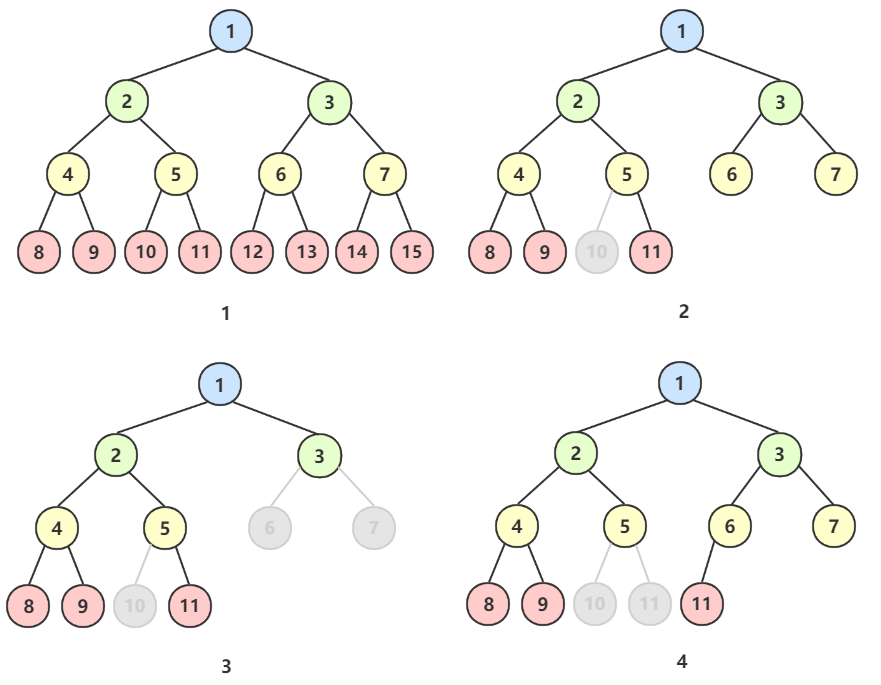
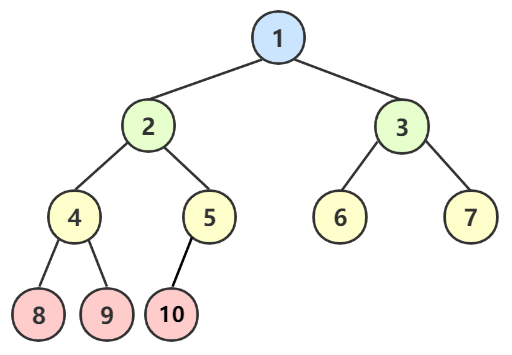
第 2 棵树虽然有些结点没有连续，但是因为每个结点都是按层序编号，和满二叉树能对应，所以是完全二叉树

第 3 棵树由于叶结点出现在最后一层（编号 8、9、10）和倒数第三层（编号 3），叶子结点层数差超过 1，所以不是完全二叉树

第 4 棵树应为 12 的结点编号为 11，所以不是完全二叉树。

完全二叉树的特点：

叶子结点只能出现在最下面两层。
最下层的叶子一定集中在左部连续位置。
倒数两层，若有叶子结点，一定都在右部连续位置
如果结点度为 1，则该结点只有左孩子，不能只有右孩子。
同样结点数的二叉树，完全二叉树的深度最小。

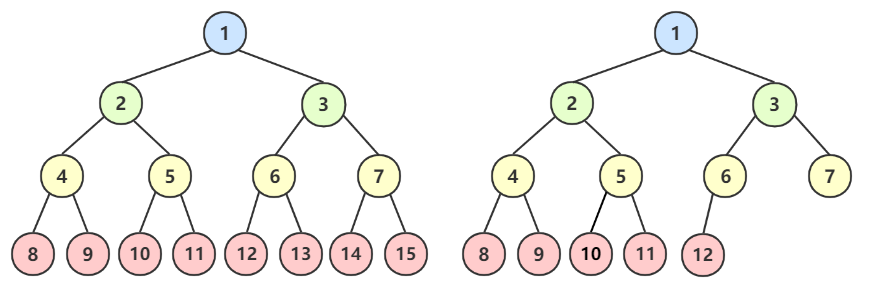
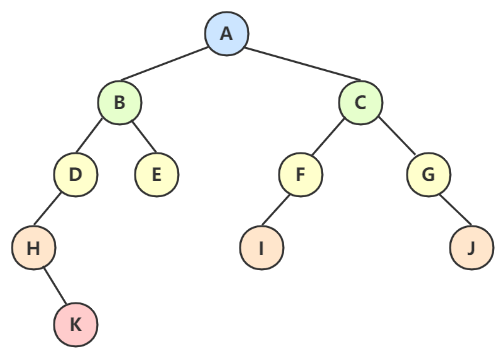
上图这两颗就是正确的完全二叉树。

左边为满二叉树，右边为完全二叉树。

看右边那棵，叶结点只在最下两层（7、8、9、10、11、12），度为1时只有左孩子（6 -> 12）

性质¶

Note

性质1性质2性质3性质4性质5

在二叉树的第 i 层上最多有 \(2^{i-1}\) 个结点。

第一层是根结点，只有1个结点，\(2^{1-1} = 2^0 = 1\)

第二层最多有2个结点，\(2^{2-1} = 2^1 = 2\)

第三层最多有4个结点，\(2^{3-1} = 2^2 = 4\)

第四层最多有8个结点，\(2^{4-1} = 2^3 = 8\)

通过归纳法，可以得出：二叉树的第i层最多有 \(2^{i-1}\) 个结点。

Tip

推广一下：一棵树的度为 n 时，又称 n 叉树。

如果一棵三叉树、四叉树，在第i层上最多有 \(3^{i-1}\)、\(4^{i-1}\) 个结点。

由此可得：一棵 n 叉树在第i层上最多有 \(n^{i-1}\)个结点。

深度为 k 的二叉树总结点数最多有 \(2^k - 1\)个（k >= 1）。

如果有一层，最多共1个结点。\(2^1 - 1 = 1\)

如果有两层，最多共3个结点。\(2^2 - 1 = 3\)

如果有三层，最多共7个结点。\(2^3 - 1 = 7\)

如果有四层，最多共15个结点。\(2^4 - 1 = 15\)

通过归纳法，可以得出：深度为 k 的二叉树总结点数最多有 \(2^k - 1\) 个。

对任何一棵二叉树 T，如果其叶子结点总数为 \(n_0\)，度为 2 的结点总数为 \(n_2\)，则 \(n_0 = n_2 + 1\)。

例如上图右边的完全二叉树，叶子结点为7、8、9、10、11、12共6个，

所以 \(n_0 = 6\)；而度为2的结点1、2、3、4、5共5个，\(n_2 = 5\)。

所以 \(n_0 = n_2 + 1 = 5 + 1 = 6\)。

总结点数为 n 的完全二叉树的深度为 \(⌊log_2 n⌋ + 1\)。 ⌊x⌋ 表示对 x 向下取整。

例如上图左边的满二叉树，总结点数为 15，深度为 \(⌊log_2 15⌋ + 1 = 4\)。

若对一颗总结点数为 n 的完全二叉树（其深度为 \(⌊log_2 n⌋ + 1\)）的结点按层序编号，对任一结点 i （1 <= i <= n）有：

如果 i = 1，则结点 i 是二叉树的根，无双亲；
如果 i > 1，则其双亲结点是第 \(⌊i/2⌋\) 个；
如果 2i > n，则结点 i 无左孩子（结点 i 为叶子结点）；否则其左孩子是结点 2i；
如果 2i+1 > n，则结点 i 无右孩子；否则其右孩子是结点 2i+1。

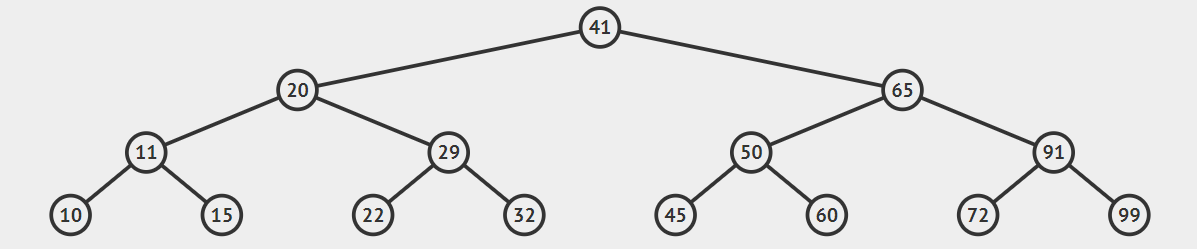
例如这样一棵完全二叉树。总结点数 10；高度 4。

如果 i = 1，根节点。
如果 i = 7，双亲就是 \(⌊7/2⌋ = ⌊3.5⌋ = 3\)；
如果 i = 6，(2i = 2*6 = 12) > (10 = n)，所以6无左孩子；
如果 i = 4，(2i + 1 = 9) > 10，所以4的右孩子是9。

总结一下就是：

i = 1，为根结点
i 的双亲是 ⌊i/2⌋
i 的左孩子是 2i
i 的右孩子是 2i + 1

存储结构¶

顺序结构适用性不强，还是用链表结构比较好。

每个结点包含一个数据域和两个左右孩子指针域，当然也可以包含一个双亲域。

typedef struct {
    int id;
    char* name;
} Elem;

typedef struct BTNode{
    Elem data;            // 数据域
    struct BTNode* lchild; // 左孩子
    struct BTNode* rchild; // 右孩子
} BTNode;

typedef struct {
    BTNode* root; // 根结点
    int depth;    // 树的度
    int count;    // 总结点数
} BTree;

遍历¶

前序遍历法 DLR中序遍历法 LDR后序遍历法 LRD层序遍历法

即先打印根结点，再打印左孩子，最后打印右孩子，以此类推

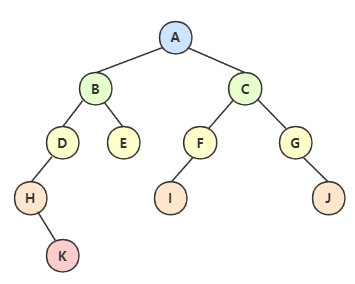
上面的打印顺序为：ABDHKECFIGJ

void PreOrderTraverse(BTNode T) {
    if (T == NULL) return;
    printf("%c", T->data);
    PreOrderTraverse(T->lchild);
    PreOrderTraverse(T->rchild);
}

即先打印左孩子，再打印根结点，最后打印右孩子，以此类推

上面的打印顺序为：HKDBEAIFCGJ

void InOrderTraverse(BTNode T) {
    if (T == NULL) return;
    InOrderTraverse(T->lchild);
    printf("%c", T->data);
    InOrderTraverse(T->rchild);
}

即先打印左孩子，再打印右孩子，最后打印根结点，以此类推

上面的打印顺序为：KHDEBIFJGCA

void PostOrderTraverse(BTNode T) {
    if (T == NULL) return;
    PostOrderTraverse(T->lchild);
    PostOrderTraverse(T->rchild);
    printf("%c", T->data);
}

即按层从左到右依次打印

上面打印顺序为：ABCDEFGHIJK

层序遍历时需要借助一个队列来完成。从根结点开始，当一个结点出队时，将其所有孩子结点入队。

void SequenceTraverse(BTree T) {
    EnQueue(T->root);
    BTNode* root = DeQueue()
    for (int i = 0; i < T->count; i++) {
        if (root) printf("%c", root->data);
        if (root->lchild) EnQueue(root->lchild);
        if (root->rchild) EnQueue(root->rchild);
    }
}

总结¶

前序就是根结点在前面

中序就是根结点在中间

后序就是根结点在后面

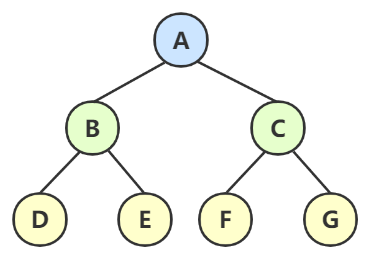
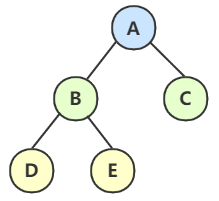
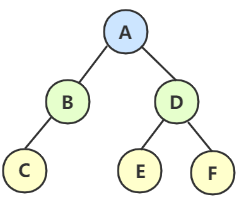
像这棵比较小的树，

前序 DLR：ABDEC
中序 LDR：DBEAC
后序 LRD：DEBCA
层次遍历：ABCDE

例题¶

如果一棵二叉树的前序遍历序列为 ABCDEF，中序遍历序列为 CBAEDF，请问后序遍历序列为？

解题思路：

前序的第一位或后序的最后一位，一定是根节点，所以这题的根结点就是 A。
接着看 A 在中序序列的位置，可以看出 CB 是 A 的左孩子，EDF是 A 的右孩子；然后在前序中就可以确定 BC 为一组，DEF 为一组。
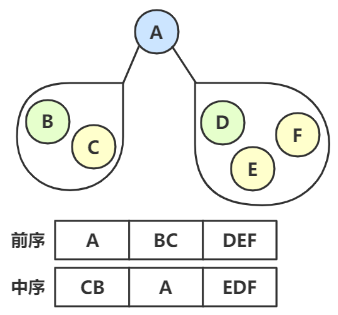
二叉树的子树也是二叉树。根据这个道理，从前序中可以知道 B是左子树的根结点，同理D是右子树的根结点。
拿着 B 和 D 到中序序列中分析，分出左右子树，以此类推。

核心就是：从前序的第一个或后序的最后一个确定根结点，然后到中序里区分左右子树。

所以这道题应该是这样一棵树：

后序应该为： CBEFDA

线索二叉树 Threading Tree¶

线索二叉树 = （前 | 中 | 后）遍历 + 二叉树

虽然采用链式结构存储，每个结点存储本身数据和左右孩子的指针，但还是会带来一个问题：叶子结点没有子树，它们的孩子指针必然为 NULL，叶子越多，NULL 越多，这就导致不管什么树，都必然会浪费一定的空间。

例下图：

现在思考如何将那些 ^ 利用起来。

如果一个结点没有孩子，则让孩子指针指向双亲？这样有的指有的不指，很奇怪，且实现起来很不方便。

如果结合遍历顺序怎么样？可以。

因为在没有遍历的情况下，我们不知道一个结点的前驱是谁，后继是谁，不如在创建树时，如果没有子树，就换成记录前驱元素或后继元素。

这样创建出来的树，就叫线索二叉树。

线索二叉树的核心思想为：

如果有左子树，则左指针域指向左子树；如果没有左子树，则左指针指向 遍历前驱元素
如果有右子树，则右指针域指向右子树；如果没有右子树，则右指针指向 遍历后继元素

这里的前驱和后继指的是某个结点在遍历后得到的序列中的前驱和后继。

例如：

后序遍历得到序列：CBEFDA。其中 E 是 F 的前驱，D 是 F 的后继。

即：线索二叉树 = （前 | 中 | 后）遍历 + 二叉树。

我们在将左右指针指向子树还是前驱后继这个行为叫做 线索化。

实现细节¶

定义了二叉树，我们需要讨论：如何知道一个结点的孩子指针是指向子树还是指向前驱后继？

为了解决这个问题，还需要在每个结点中增加两个变量 ltag 、rtag。

当 ltag 或 rtag 为 true 时表示有孩子，指针域指向子树；当 ltag 或 rtag 为 false 时表示没有孩子，指针域指向前驱或后继。

typedef struct BTNode{
    Elem data;             // 数据域
    struct BTNode* lchild; // 左孩子
    struct BTNode* rchild; // 右孩子
    bool ltag;
    bool rtag;
} BTNode;

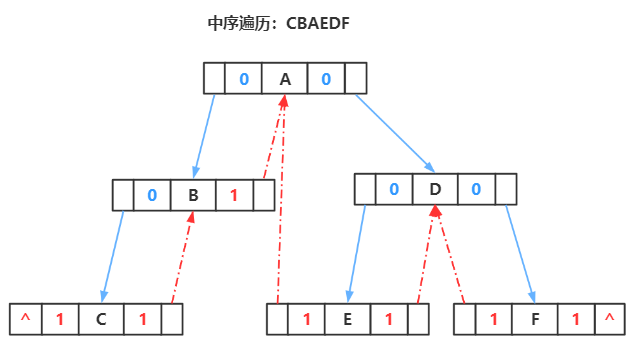
这样在创建一棵树时，如果某个结点有左子树，ltag 为 true，lchild 指向左子树；如果没有左子树，ltag 为 false，lchild 指向前驱。 eg：

这样一棵二叉树，经过中序线索化以后，变成下面这样：

TTNode* pre;     // 全局变量，指向刚刚访问过的结点
void InThreading(TTNode* T) {
    if(T) {
        InThreading(T->lchild);    // 递归左子树线索化

        /** 线索化 begin */
        if(!T->lchild) {    // 没有左孩子
            T->ltag = false;        // 线索标志
            T->lchild = pre;    // 指向前驱元素
        }
        if(!pre->rchild) {    // 前驱结点没有右孩子
            pre->rtag = false;      // 线索标志
            pre->rchild = T;    // 前驱右指针指向当前指针
        }
        pre = T;    // 保持 pre 指向 T 的前驱
        /** 线索化 end */

        InThreading(T->rchild);    // 递归右子树线索化
    }
}

转换¶

树转二叉树¶

一棵不规则的树，在一定程度上可以转换为一棵二叉树。

转换方法：

连接：兄弟之间连线
断开：双亲结点只保留最左孩子，其余都断开
旋转：调整好位置
保留的做左子树，连接的做右子树

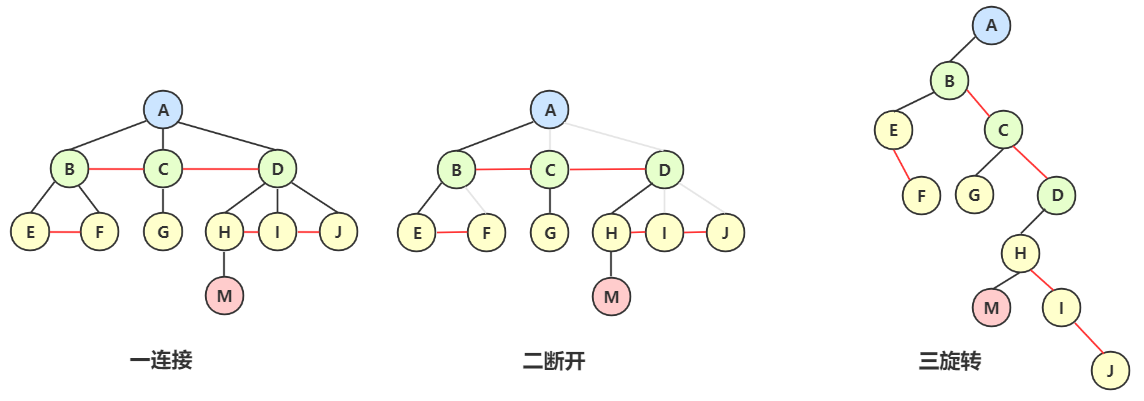
将这样一棵树转成二叉树。

树转二叉树

第一步：兄弟结点之间连接起来。例如 BCD 之间都连接起来了。
第二步：除了双亲跟左孩子，其他联系都断开。例如A只保留与 B，断开与 CD 的关系。
第三步：旋转调整。保留下来的作为左子树，连接得来的作为右子树。例如 B 是保留下来的，作为左子树，CD 是连接出来的，作为右子树。

Tip

口诀：一连接、二断开、三旋转、保留左子树、连接右子树。

二叉树转树¶

二叉树转树是树转二叉树的逆过程

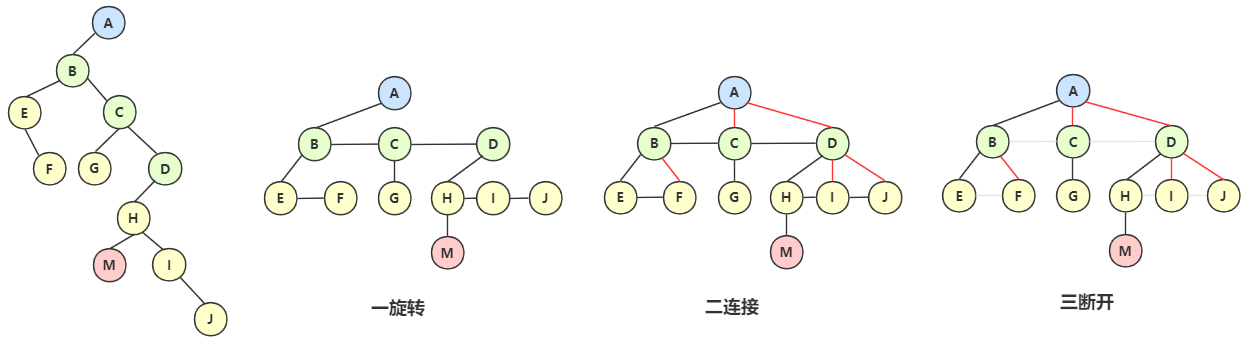
一旋转、二断开、三连接即可。

二叉树转树

第一步：旋转，将右子树都旋转都同一层
第二步：连接右子树结点与双亲结点
第三步：断开兄弟间的连线

二叉树转森林¶

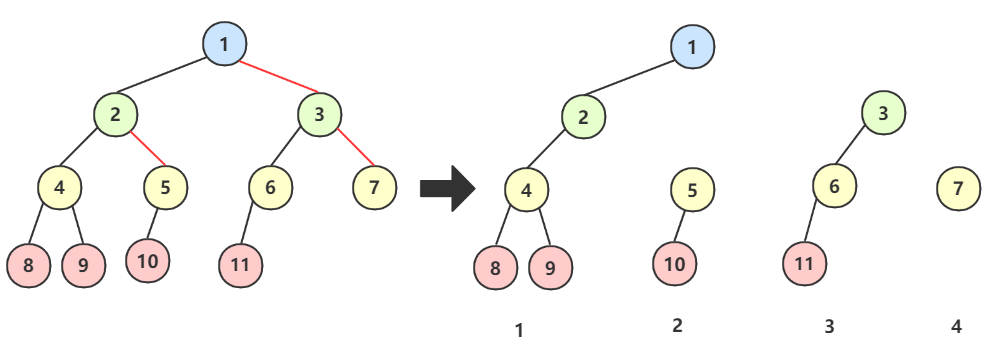
判断一棵树是普通树还是二叉树，看它根结点有没有右子树。有就是二叉树，没有就是普通树。

二叉树转森林只需要把每个 有孩子的右子树 拆开作为单独一棵树即可。

二叉树转森林

哈夫曼树¶

哈夫曼树是一类带权路径长度最短的树，又称赫夫曼树、最优树、最优二叉树。

哈夫曼树的应用非常广泛，特别是在大文本编码方面，压缩比非常可观。

首先解释一下带权路径：

路径：两个结点之间那根线就叫路径
权：路径上的数字。
带权路径：两个结点之间那根线带数字

带权树

权值可以用来表示某些含义，而在哈夫曼编码中，权值只有 0 和 1 两种。

路径长度：从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称作路径长度
树的路径长度：从树根到每一个结点的路径长度之和。
树的带权路径长度：树中所有叶子结点的带权路径长度之和，

通常记作 \(WPL=\sum^n_{k=1}{w_kl_k}\)。（\(l\) 为结点 \(k\) 的层数，从 0 开始计算）

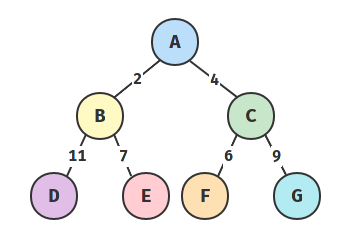
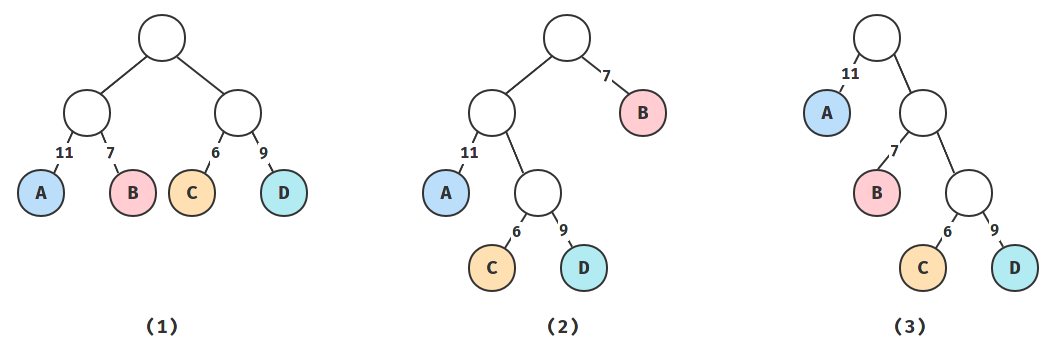
上图中的 3 棵二叉树，都有 4 个叶子结点 A、B、C、D，分别带权 11、7、6、9。

他们的带权路径长度分别为：

\(WPL = 11 \times 2 + 7 \times 2 + 6 \times 2 + 9 \times 2 = 66\)
\(WPL = 11 \times 2 + 7 \times 1 + 6 \times 3 + 9 \times 3 = 74\)
\(WPL = 11 \times 1 + 7 \times 2 + 6 \times 3 + 9 \times 3 = 70\)

假设有一棵二叉树，其有 n 个叶子结点，并有 n 个权值 \({w_1, w_2, ..., w_n}\)，每个叶子结点带权为 \(w_i\)，则其中带权路径长度 WPL 最小的二叉树称作最优二叉树或哈夫曼树。

哈夫曼编码¶

哈夫曼编码是一种变长的编码方式，在大文本压缩方面有着出色的表现。

相对比变长，另一种编码方式为定长。

假设现在有一串文本 aaabbaacdeefdeaeff，共 18 个字符。

现在要进行远距离传输，我们需要先进行编码，也就是编成二进制形式。

可以看到总共是 abcdef 这几个字符，那么我们可以用 001 表示 a，010 表示 b，011 表示 c... 以此类推。

a	b	c	d	e	f
001	010	011	100	101	110

这就是定长编码，每一个字符编码后都是同样的位数 3 位。

aaabbaacdeefdeaeff 编码后为 001001001010010001001011100101101110100101001101110110。18 个字符共编成 54 个二进制位。

这种方式有个缺点：现在只有 6 种字符，所以每个字符编码后的位数占了 3 位，如果有 17 种字符，那么每个字符编码后需要占用 5 位，非常浪费空间。

所以哈夫曼教授提出了现在的哈夫曼编码，核心就是一句话：让出现次数越高的字符占用越少的位数。

编码步骤¶

这是一种变长的编码方式，具体步骤如下：

统计各种字符的出现次数构成一个序列
对序列进行排序
选取 2 个最小的作为叶子结点，父结点为两次数之和
将选出的两个数从序列中删除，将父结点加入序列
重复步骤 2，直到序列为空。

注意事项：

保持任何左侧结点都比右侧的兄弟结点小/大。
构造完成以后，给每一条路径填充权值 0 或 1。

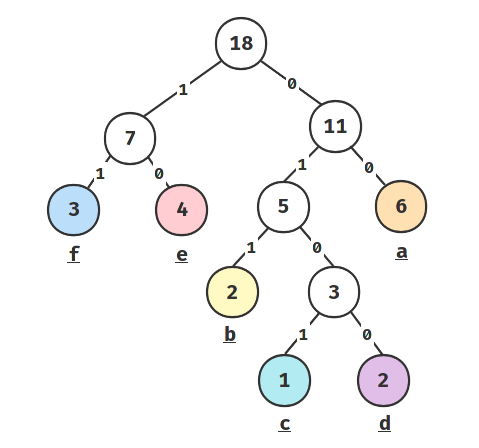
上面的例子用哈夫曼编码，应该是这样：

最终会生成一颗这样的树：

然后从根结点开始，直到字符那个结点，这一路的权值拼接起来就得到了变长编码。

a	b	c	d	e	f
00	011	0101	0100	10	11

现在，aaabbaacdeefdeaeff 编码后为 00000001101100000101010010101101001000101111。18 个字符共编成 44 个二进制位。

压缩比为 \(44 \div 54 = 81\)%。

看起来不多，但是计算机中一个字符需要 8 个位存储，18 个字符共 144 位。

这样算下来压缩比直接达到 \(44 \div 144 = 30\)%！

代码实现¶

伪代码

while (序列长度 >= 1) {
    将序列排序
    栈顶 2 个元素出栈
    构造子树
    将父结点的值入栈
}
填充权值

DataElement.hHuffman.hHuffman.cmain.c

// DataElement.h

#ifndef DATAELEMENT_H_INCLUDED
#define DATAELEMENT_H_INCLUDED

#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 10

typedef struct Node {
    char data;
    int value;
    struct Node* lNode;
    struct Node* rNode;
    int lWeight;
    int rWeight;
} Node;

typedef struct Stack {
    Node* datas[MAXSIZE];
    int top;
} Stack;

typedef struct {
    char data;
    int times;
} seq;

#endif

// Huffman.h

#ifndef HUFFMAN_H_INCLUDED
#define HUFFMAN_H_INCLUDED

#include <stdbool.h>
#include "DataElement.h"
#define len(x) sizeof(x)/sizeof(x[0])


// 将序列排序
bool sort(Stack*);

// 出栈两个元素
void pop(Stack* s, Node* nodeArr[2]);

// 构造子树
Node* buildSubTree(Node* nodeArr[2]);

// 父结点入栈
void push(Stack* s, Node* parent);

bool initStack(Stack* s, seq arr[], int arrLen);
void printStack(Stack* s);
void frontPrint(Node* root);
void midPrint(Node* root);
void stuffWeight(Node* root);

#endif

// Huffman.c

#include "Huffman.h"

// 将序列排序
/**
* @name 直接插入排序算法
* 循环数组长度 -1 次，每次循环将当前目标数与前面部分（已排好序）比较
* 前一个数大于当前数则交换位置，一直比较一直换，直到前面的数小于当前数时，退出比较，换下一个目标数继续比较。
*/
bool sort(Stack* s)
{
    int i;
    for (i = 1; i < s->top + 1; i++) { // 一共循环数组长度 -1 次
        int j;
        for (j = i; j > 0; j--) {
            Node* prev = s->datas[i - 1];
            Node* curr = s->datas[i];
            if (prev->value < curr->value) { // 若前一个小于后一个，则交换两个结点，当前目标数位置-1
                Node* tmp = s->datas[i - 1];
                s->datas[i - 1] = s->datas[i];
                s->datas[i] = tmp;
                tmp = NULL;
                i--;
            } else {
                break;
            }
        }
    }
}

// 出栈两个元素
void pop(Stack* s, Node* nodeArr[2])
{
    nodeArr[0] = s->datas[s->top--];
    nodeArr[1] = s->datas[s->top--];
}

// 构造子树
Node* buildSubTree(Node* nodeArr[2])
{
    Node* parent = (Node*)malloc(sizeof(Node));
    parent->data = '-';
    parent->value = nodeArr[0]->value + nodeArr[1]->value;
    parent->lNode = nodeArr[0];
    parent->rNode = nodeArr[1];
    parent->lWeight = parent->rWeight = -1;
    return parent;
}

// 父结点入栈
void push(Stack* s, Node* parent)
{
    s->datas[++s->top] = parent;
}

// 填充每条路径上的权值
void stuffWeight(Node* root)
{
    if (root) {
        if (root->lNode)
            root->lWeight = 1;
        if (root->rNode)
            root->rWeight = 0;
        stuffWeight(root->lNode);
        stuffWeight(root->rNode);
    }
}

// 初始化栈
bool initStack(Stack* s, seq arr[], int arrLen)
{
    int i;
    for (i = 0; i < MAXSIZE; i++)
        s->datas[i] = NULL;

    s->top = -1;

    // 将数组填充进栈里
    for (i = 0; i < arrLen; i++) {
        Node* node = (Node*)malloc(sizeof(Node));
        node->data = arr[i].data;
        node->value = arr[i].times;
        node->lNode = node->rNode = NULL;
        node->lWeight = node->rWeight = -1;
        push(s, node);
    }
    return true;
}

// 前序遍历打印
void frontPrint(Node* root)
{
    if (root != NULL) {
        printf("%c %2d; %2d, %2d\n", root->data, root->value, root->lWeight, root->rWeight);
        frontPrint(root->lNode);
        frontPrint(root->rNode);
    }
}

// 中序遍历打印
void midPrint(Node* root)
{
    if (root != NULL) {
        midPrint(root->lNode);
        printf("%c %2d; %2d, %2d\n", root->data, root->value, root->lWeight, root->rWeight);
        midPrint(root->rNode);
    }
}

// main.c

#include "Huffman.c"
#include "tools.c"

void BuildHuffman()
{

    seq arr[] = { { 'a', 6 }, { 'b', 2 }, { 'c', 1 }, { 'd', 2 }, { 'e', 4 }, { 'f', 3 } };
    Stack s;
    initStack(&s, arr, len(arr));
    Node* popArr[2];

    while (s.top >= 1) {
        sort(&s);
        pop(&s, popArr);
        Node* parent = buildSubTree(popArr);
        push(&s, parent);
    }
    stuffWeight(s.datas[s.top]);
    printStack(&s);
    frontPrint(s.datas[s.top]);
    printf("\n");
    midPrint(s.datas[s.top]);
}

void main()
{
    BuildHuffman();
}