7-图

图 是有顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G（ V, E ）

其中 G 表示一个图，V 是顶点集合，E 是边的集合。

• 线性表的数据元素 -> 元素 Element
• 树中的数据元素 -> 结点 Node

• 图中的数据元素 -> 顶点 Vertex¹

• 线性表没有数据元素 -> 空表

• 树中没有数据元素 -> 空树
• 图中没有数据元素 -> 不行！

线性表中，相邻的元素之间具有线性关系

树中，相邻的两层之间具有层次关系

图中，任意两个顶点之间都可能有关系。顶点之间的逻辑关系用边来表示。边集可以为空。

定义

无向边

若顶点 vi 到 vj 之间的边没有方向，则称这条边为无向边（Edge）²，用 无序偶对（vi, vj） 来表示。

如果图中任意两个顶点之间的边都是无向边，则称该图为无向图（Undirected graphs）³。

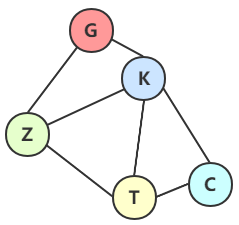
上图就是一个无向图，K 到 T 之间的边可以表示成无序对（K, T）或者（T, K）。 而整个图可以描述成为: G1 = (V1，{E1})， 其中顶点集合 V1={G, Z, K, T, C}； 边集合 E1 = { (G, Z), (G, K), (Z, K), (Z, T), (K, T), (K, C), (T, C) }；

有向边

若顶点 vi 到 vj 之间的边有方向，则称这条边为弧（Arc）⁴。

用 无序偶对 来表示： \(v_i \to v_j\)，

vi 称为弧尾（Tail），即指出去的那个； vj 称为弧头（Head），即被指的那个。

如果图中任意两个顶点之间的边都是有向边，则称该图为有向图（Directed graphs）⁵。

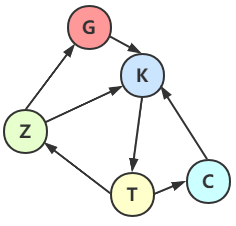
上图就是一个有向图，连接 G 到 K 的边就是弧，K 是弧头，被指向的那个，G 是弧尾，指出去的那个。

表示弧，不能写为 。

而整个图可以描述成为 G2 = (V2，{E2})，

其中顶点集合 V2 = {G, Z, K, T, C}；

弧集合 E2 = { <G, K>, <Z, G>, <Z, K>, <K, T>, <T, Z>, <T, C>, <C, K> }；

Warning

注意：无向边用 () 表示， 有向边用 < > 表示。

简单图

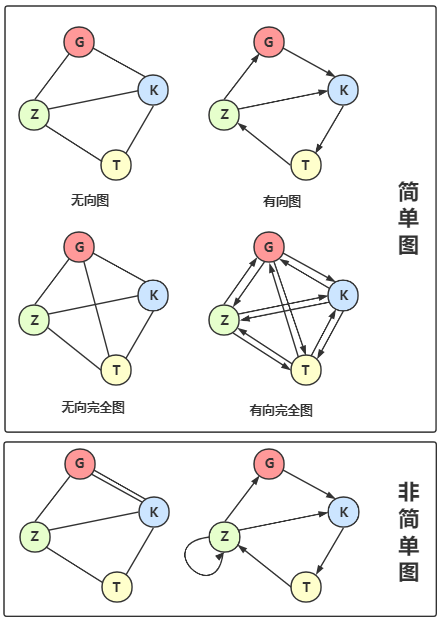
在图中若不存在顶点到其自身的边，且同一条边不重复出现，则称这样的图为简单图⁶。

在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图（Undirected Completed graph）⁷

在有向图中，如果任意两个顶点之间都存在方向互为相反的两条弧，则称该图为有向完全图（Directed graph）。⁸

含有 n 个顶点的无向完全图有 \(\frac {n(n-1)} 2\) 条边，如上图的无向完全图有4个顶点，边数为 \(4 \times 3 \div 2 = 6\)

含有 n 个顶点的有向完全图有 \(n \times (n-1)\) 条边，如上图的有向完全图有4个顶点，边数为 \(4 \times 3 = 12\)

Tip

推广一下：

在非完全的图中，设图具有 n 个顶点和 e 条边，

若该图为无向图则 \(0 \leq e \leq \frac {n(n-1)} 2\)

若该图为有向图则 \(0 \leq e \leq n(n-1)\)

有很少条边或弧称为 稀疏图（Sparse greph），反之称为 稠密图（Dense greph）。稀疏和稠密的相对的概念，没有严格定义。

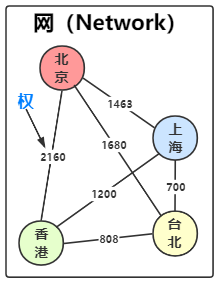
权、网

图的边或弧有相关的数值，这个数叫做权（Weight）⁹，可以表示一个顶点到另一个顶点的距离或耗费等等。 这种带全的图通常称为网（Network）¹⁰。

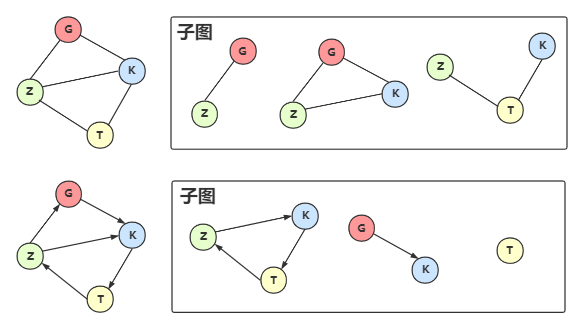
子图

假设两个图 \(G = (V, {E})\) 和 \(G' = (V', {E'})\)，如果 \(V' \subseteq V\) 且 \(E' \subseteq E\)，则称 G' 为 G 的子图（Subgraph）¹¹。

图的顶点和边间的关系

度

无向图的度

对于无向图 G = (V, {E})

• 如果边 \((v, v') \in E\)，则称顶点 \(v\) 和 \(v'\) 互为 邻接点（Adjacent），即 \(v\) 和 \(v'\) 相邻接。
• 边 \((v, v')\) 依附（Incident） 于顶点 \(v\) 和 \(v'\)，即边 \((v, v')\) 与顶点 \(v\) 和 \(v'\) 相关联。
• 顶点 \(v\) 的度（Degree）¹² 是和 \(v\) 相关的边的数量，记为 \(TD(v)\)。

eg:

例如这个图，顶点 \(G\) 和 \(K\) 互为邻接点，边 \((G, K)\) 依附于 \(G\) 和 \(K\) 上，\(K\) 顶点的度为 3。

图的边数为 5，各个顶点的度的和 = 3+3+2+2 = 10，其中重复两次计数，所以 边数应为个顶点度数之和的一半。

记作

\[e= \frac 1 2 \sum_{i=1}^n TD(v_i)\]

有向图的度

对于有向图 G = (V, {E})

• 如果弧 \(\langle v, v' \rangle \in E\)，则称：顶点 \(v\) 邻接到 \(v'\)，顶点 \(v'\) 邻接自 \(v\)。顶点 \(v\) 和 \(v'\) 互为 邻接点（Adjacent）。
• 弧 \(\langle v, v' \rangle\) 依附（incident） 于顶点 \(v\) 和 \(v'\)，即弧 \(\langle v, v' \rangle\) 与 顶点 \(v\) 和 \(v'\) 相关联。
• 以顶点 \(v\) 为头的弧的数量称为 \(v\) 的入度（InDegree）¹³，记为 \(ID(v)\);
• 以顶点 \(v\) 为尾的弧的数量称为 \(v\) 的出度（OutDegree）¹⁴，记为 \(OD(v)\);
• 顶点 \(v\) 的 度（Degree） 为 \(TD(v) = ID(v) + OD(v)\)。

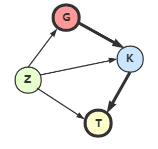
例如 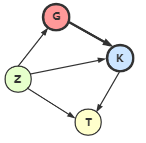这个图，顶点 \(G\) 和 \(K\) 互为邻接点，顶点 \(G\) 邻接到 \(K\)，\(K\) 邻接自 \(G\)。

边 \((G, K)\) 依附于 \(G\) 和 \(K\) 上，顶点 \(K\) 的入度为 2，\(ID(K) = 2\)，出度为 1，\(OD(K) = 1\)，度为 \(TD(K) = ID(K) + OD(K) = 3\)

图的弧数为 5，各个顶点的入度和 = 1+2+2+0 = 5，出度和 = 1+1+0+3 = 5；

由此可得有向图的弧数:

\[e= \sum_{i=1}^n ID(V_i) = \sum_{i=1}^n OD(v_i)\]

路径

无向图 \(G = (V, {E})\) 中从顶点 \(v\) 到顶点 \(v'\) 的路径（Path）¹⁵是一个顶点序列 \((v = v_{i,0}, v_{i,1}, ..., v_{i,m} = v')\)，其中 \((v_{i,j-1}, v_{i,j}) \in E, 1\leq j \leq m\)。

G 到 T 有四种路径

如果 G 是有向图，则路径也是有向的，顶点序列应满足 \(\langle v_{i,j-1}, v_{i,j}\rangle \in E, 1 \leq j \leq m\)。

G 到 T 只有一种路径，其他路径都不行。因为 G 到 Z 不存在路径。

路径的长度¹⁶是路径上的边或弧的数量。例如上图的有向图，G到T的路径长度为2。

第一个顶点到最后一个顶点相同的路径称为回路（circuit）或环（Cycle）¹⁷。

序列种顶点不重复出现的路径为简单路径¹⁸。

除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路，称为 简单回路（Simple circuit） 或 简单环（Simple Cycle）。

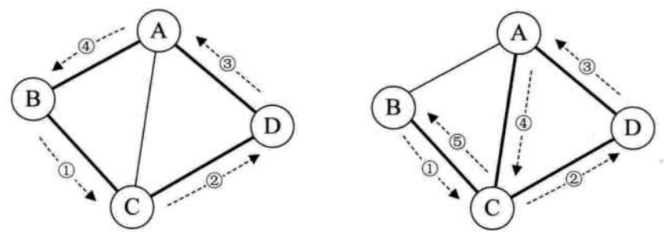
左边图路径为 {B, C, D, A, B}，第一个顶点和最后一个顶点都是 B，且 C、D、A没有重复出现，所以是一个简单环。

右边图路径为 {B, C, D, A, C, B}，由于 C 重复，所以不是简单环。

连通图

无向连通图

无向图中：

任意两个顶点之间都有 直接或间接 的路径，即都能到达，则称这个图为连通图（Connected Graph）¹⁹。

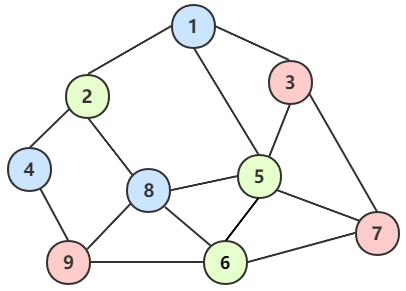
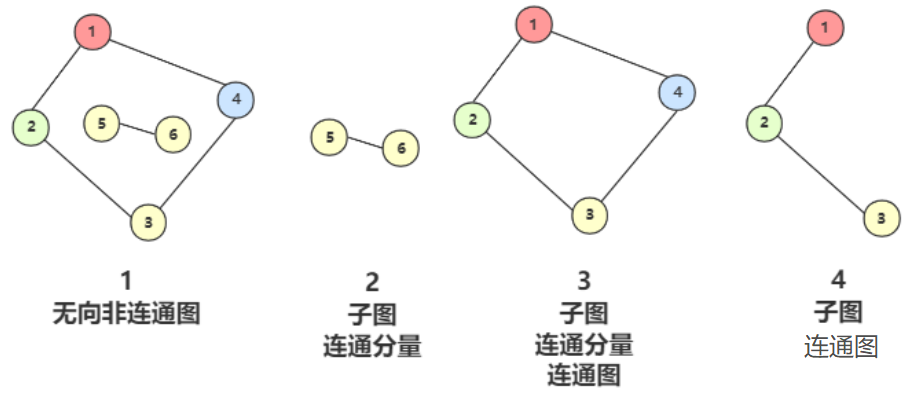
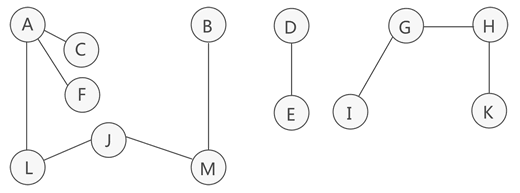
例如 图1 就是非连通图，应为顶点 5 和 6 没有路径到顶点 1、2、3、4，而图2、3、4 就是连通图。

无向图中的 极大连通子图（Great Connected Subgraph） 称为连通分量（Connected Component）²⁰，它强调：

• 必须是子图（子图）
• 子图是连通的（连通）
• 连通子图含有极大顶点数（有极大顶点数）
• 具有极大顶点数的连通子图包含依附于这些顶点的所有边。（含有边）

例如 图1就是一个无向非连通图，但是它有两个连通分量 图2 和 图3，而 图4 虽然是 图1 的子图，但是不满足连通子图的极大顶点数（图2 满足），所以不是连通分量。

有向连通图

有向图中：

任意两个顶点都有直接路径或间接路径，则称这个图为强连通图（Strong Connected Graph）²¹。

有向图中的 极大强连通子图（Great Strong Connected Subgraph） 称作有向图的强连通分量（Strong Connected Component）²²。

例如 图1 就不是一个强连通图，因为 1 到 4 有路径，而 4 到 1 没路径。而 图2 就是 图1 的极大强连通子图，即它的强连通分量。

生成树、生成森林

生成树

Note

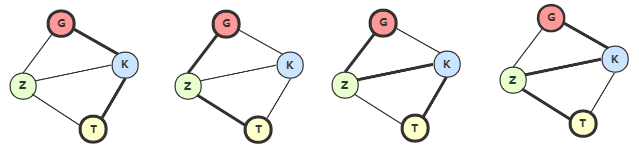
对连通图进行遍历，过程中所经过的边和顶点的组合可看做是一棵普通树，通常称为生成树（Spanning Tree）²³。

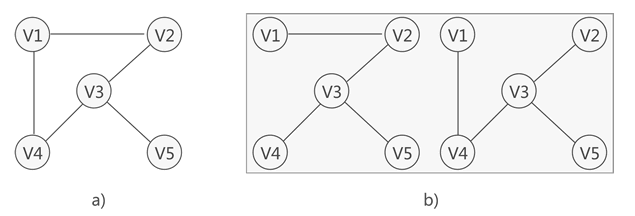
左边是一张连通图，右边则是其对应的两种生成树。 连通图中，任意两顶点之间可能还有多条路径，遍历连通图的方式有多种，往往一张连通图可能有多种不同的生成树与之对应。

Note

连通图中的生成树必须满足以下2个条件：

1. 包含连通图中所有的顶点；
2. 任意两顶点之间有且仅有一条通路；

因此，连通图的生成树具有这样的特征：生成树中 边的数量 = 顶点数 - 1。

\[ \begin{cases} 非连通图, & 顶点个数 = n;边数 \lt n-1 \\\\ 生成树, & 顶点个数 = n;边数 = n-1 \\\\ 一定有环, & 顶点个数 = n;边数 \gt n-1 \\\\ \end{cases} \]

生成森林

Note

生成树的对于连通图来说的，而生成森林则是对应非连通图来说的。

非连通图可以分解为多个连通分量，而每个连通分量又各自对应多棵生成树，因此与整个非连通图相对应的，是由多棵生成树组成的生成森林（Spanning Forest）²⁴。

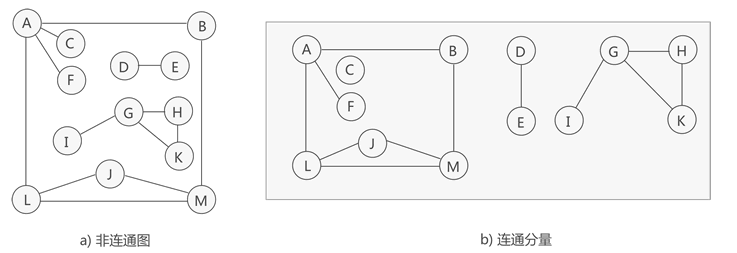
上图左边是一张非连通图，可以分解为右边三个连通分量，其中各个连通分量对应的生成树如下所示：

上图只是列出各个连通分量的其中一种生成树。

总结

• 图由顶点和边组成，无向图由 顶点 和 边 构成；有向图由 顶点 和 弧 构成，弧分 弧头弧尾。
• 任两个顶点之间都存在边叫 完全图，分 有向完全图 和 无向完全图。同一条边不重复出现的图叫 简单图。
• 顶点之间有 邻接点、依附 的概念，无向图的顶点的边数叫 度，有向图的顶点分 出度 和 入度 ，度 = 出+入。
• 从图的顶点集和边集中取一小部分组成新的图，称为原图的 子图。
• 带数值的边叫 权，顶点和权构成 网
• 图中顶点间存在 路径，两顶点存在路径则说明是 连通 的，如果路径最终回到起始点则称为 环，当中顶点没有重复过称为 简单路径。若任意两顶点都是连通的，则图是 连通图，有向则是 强连通图。图中有子图，若子图极大连通则称 连通分量，有向则称 强连通分量。
• 无向图中连通且边数 = 顶点数 - 1 的树叫 生成树，无向非连通图的连通分量生成的生成树一起构成 生成森林。
• 有向图中一个顶点入度为 0，其他顶点的入度为1的叫 有向树。一个有向图由若干棵有向树构成生成森林。

---

1. 顶点 -> 图的数据元素 ↩

2. 无向边 -> 边没有方向 ↩

3. 无向图 -> 边没有方向的图，n个顶点的无向图最多有 \(\frac {n(n-1)} 2\) 条边 ↩

4. 弧 -> 边有方向；弧有弧头弧尾之分 ↩

5. 有向图 -> 边有方向的图，n个顶点的有向图最多有 \(n(n-1)\) 条边 ↩

6. 简单图 -> 同一条边不重复出现的图 ↩

7. 无向完全图 -> 任意两个顶点之间都有边，共有 \(\frac {n(n-1)} 2\) 条边 ↩

8. 有向完全图 -> 任意两个顶点之间都有弧，共有 \(n(n-1)\) 条弧 ↩

9. 权 -> 有数值的边 ↩

10. 网 -> 顶点+权 ↩

11. 子图 -> 从原图中拆出来的图 ↩

12. 度 ->顶点的边数 ↩

13. 入度 -> 邻接到顶点的边的数量 ↩

14. 出度 -> 顶点邻接出去的边的数量 ↩

15. 路径 -> 两个顶点之间的直接线路或间接线路的边集序列，注意是序列，所以可能不止一条 ↩

16. 路径长度 -> 两个顶点之间的线路的边数 ↩

17. 回路或环 -> 从起始点离开最后到达起始点的路径 ↩

18. 简单路径 -> 回路上没有重复的点的路径 ↩

19. 连通图 -> 任意两顶点都是连通的无向图 ↩

20. 连通分量 -> 无向图的极大连通的子图 ↩

21. 强连通图 -> 任意两顶点都是连通的有向图 ↩

22. 强连通分量 -> 有向图的极大连通的子图 ↩

23. 生成树 -> 无向连通图生成的 边的数量 = 顶点数 -1 的树 ↩

24. 生成森林 -> 无向非连通图的连通分量生成的生成树一起构成生成森林 ↩