Skip to content

图的应用: 最小生成树、最短路径、拓扑排序、关键路径

9-图3

图在现实中有着许多的应用，帮助人们解决了许多问题，同时图的应用也是比较晦涩难懂的地方。

本文图的应用共有： - 最小生成树 - 最短路径法 - 拓扑排序 - 关键路径

从图结构的角度看，图的应用有两种：一种的解决无向图的，一种是解决有向图的。 更详细的看： - 最小生成树使用的是贪心算法，得到的是局部最优解，有可能得到的不是全局最优解 - 最短路径法使用的是动态规划，得到的是全局最优解 - 拓扑排序关注的是点 - 关键路径关注的是边

接下来每讲一个应用之前我会先举一个场景，这样学习的时候才不至于不知道用来干嘛的。

最小生成树 Minimum Spanning Tree

应用场景

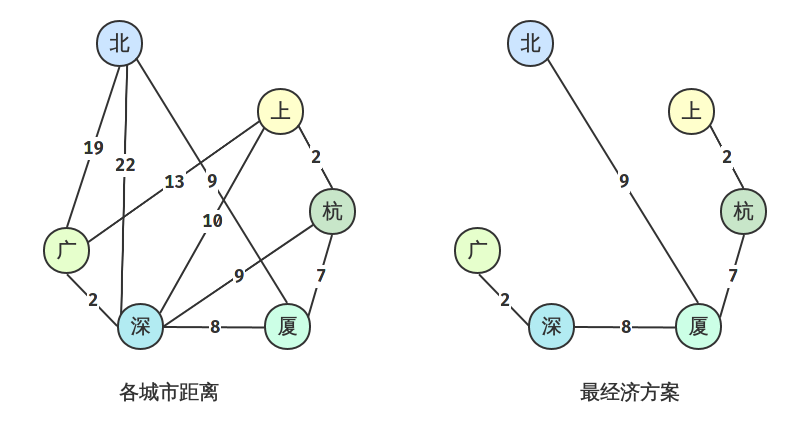
假设现在有 北、上、广、深、杭、厦 几个城市，他们之间要建立通信联络网。 一共有 6 个城市，他们之间最少只需要 6 - 1 = 5 条通信线路即可连通。 但是各个城市之间的距离是不同的，距离越远，建立费用越高（即距离和费用成正比）。 所以，问题就是：怎么样让这 6 个城市建立起通信联络网，并且建立费用最低？

答案是使用最小生成树。

理解

要理解最小生成树，可以从**最小**和**树**去理解。

先理解「树」： 首先，生成树是一颗树，那么一堆顶点要生成一棵树，就不能有环 其次，每个顶点都不能落下，所以这些顶点得组成一个连通图

接着理解「最小」： 一张网，也就是路径上带权值的图，可以有很多生成树，而最小生成树则是：所有生成树里路径权值总和最小的一颗生成树。

普里姆算法 (Prim)

从任一顶点出发，将其加入已选顶点数组、其邻接的边加入备选边数组； 选取该顶点权值最小的一条边，所连接的顶点也加入已选顶点数组，并将该边

克鲁斯卡尔算法 (Kruskal)

克鲁斯卡尔算法适合求 稀疏网 的最小生成树。

克鲁斯卡尔算法的做法是将每一条边和权值存储到数组中，然后 1. 进行一次从小到大的排序。 2. 从最小的边开始，将边放置到顶点上。放置前判断是否产生环： 1. 是：跳过这条边 2. 否：放置这条边 3. 重复步骤 1

总共放置顶点总数 - 1 次即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
typedef struct {
    Vertex a, b;
    int Weight;
} Edge;

Edge net[];

void Kruskal() {
    sort(net);
    int n = 0;
    for (size_t i = 0; i < len(net); i++) {
        if (n > VertexCount-1) break;

        if (isCycle(net[i].a)) {
            continue
         } else {
            addEdge(net[i]);
            n++;
         }
    }
}

先将每条边和其权值存储到数组里，做一个从小到大的排序 遍历数组，判断是否产生环 是：删除该边 否：将边放入图中，进入下一轮 循环次数：顶点总数 - 1

最短路径

最短路径和最小生成树都是求几个顶点之间的最短的路径，区别在于： - 最小生成树的思想是使用贪心算法，而贪心算法能获得的是局部最优解，不一定是全局最优解 - 最短路径的思想则是使用动态规划，而动态规划能获得的是全局最优解

迪杰斯特拉算法 (Dijkstra)

弗洛伊德算法 (Floyd)

拓扑排序

AOV-网 (Activity On Vertex Network)

关键路径

AOE-网 (Activity On Edge Network)