8-图2

图的ADT

ADT 图 Graph
Data
    顶点的有穷非空集合和边的集合
Operation
    CreateGraph(*G, V, E): 按照顶点集V和边集E的定义构造图G
    DestoryGraph(G*): 图G存在则销毁
    LocateVex(G*, v): 若图G中存在顶点v，则返回v在图中的顶点数组的下标
    GetVex(G*, v): 返回图中顶点v的值
    PutVex(G*, v, value): 将图G中顶点v赋值value
    FirstNeighbor(G*, v): 返回顶点v的第一个邻接点，若无则返回空
    NextNeighbor(G*, v1, v2): 返回顶点v1相对于顶点v2的下一个邻接点，若v2是v1的最后一个邻接点则返回空
    InsertVex(G*, v): 在图G中增加顶点v
    DeleteVex(G*, v): 删除图G中顶点v及其相关的边/弧
    InsertArc(G*, v1, v2): 在图G中增加弧<v1, v2>，若G是无向图，还需添加对称弧<v2, v1>
    DeleteArc(G*, v1, v2): 在图G中删除弧<v1, v2>，若G是无向图，还需删除对称弧<v2, v1>
    DFSTraverse(G*): 对图G中进行深度优先遍历
    BFSTraverse(G*): 对图G中进行广度优先遍历
    Adjacent(G*, v1, v2): 判断图G中是否存在边/弧<v1, v2>
    Neighbors(G*, v): 列出图G中与顶点v邻接的边
    GetEdgeValue(G*, v1, v2): 获取图G中边/弧<v1, v2>对应的权值
    SetEdgeValue(G*, v1, v2, value): 设置图G中边/弧<v1, v2>对应的权值为value
endADT

图的存储结构

图的顶点之间没有次序关系，且顶点的邻接情况多变，无法用统一的格式来存储。

图的存储结构总共有以下 5 种方式：

1. 邻接矩阵
2. 邻接表
3. 十字链表
4. 邻接多重表
5. 边集数组

邻接矩阵 Adjacent Matrix

Note

图的邻接矩阵的存储方式是用两个数组来表示图。

一个一维数组用来存储图中的顶点集，一个二维数组（称为邻接矩阵）用来存储图中的边集。

图的邻接矩阵表示法 = 一维数组 \(\times\) 1 + 二维数组 \(\times\) 1

设 图G 有 n 个顶点，则邻接矩阵是一个 \(n \times n\) 的方阵，定义为：

\[ Arc[i][j] = \begin{cases} 1, & {(v_i, v_j) \in E 或 \langle v_i, v_j \rangle \in E} \\\\ 0, & {反之} \end{cases} \]

无向图

理论描述

顶点集 很容易表示，使用顶点结构类型的一维数组来存储顶点信息。 边集 可以用 矩阵(Metrix) 来表示，而矩阵在计算机中可以使用二维数组来实现。

eg: { loading=lazy } 这个图的边集可以变成下面的矩阵：

\[ \begin{bmatrix} 0 & 1 & 1 & 0 \\\\ 1 & 0 & 1 & 0 \\\\ 1 & 1 & 0 & 1 \\\\ 0 & 0 & 1 & 0 \end{bmatrix} \]

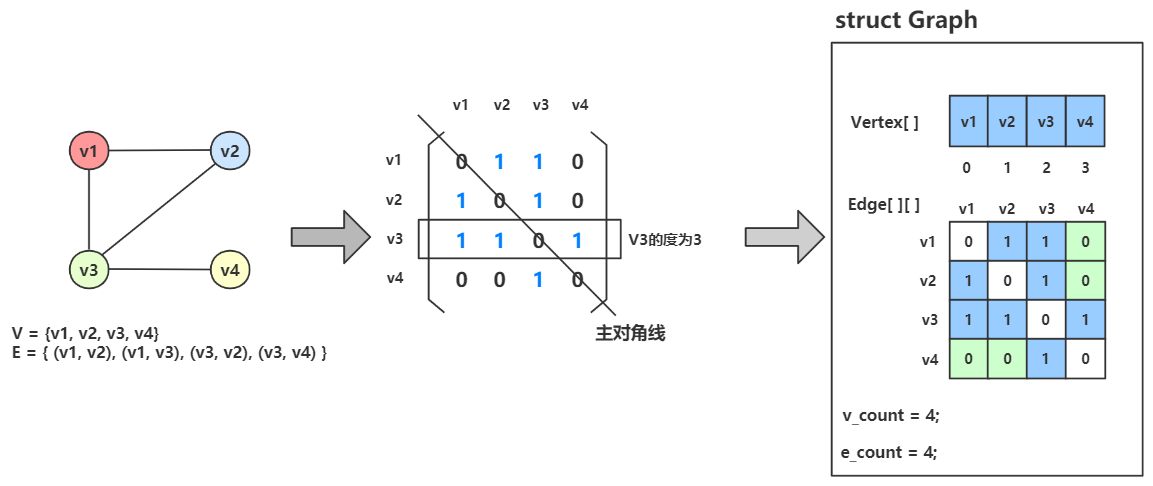
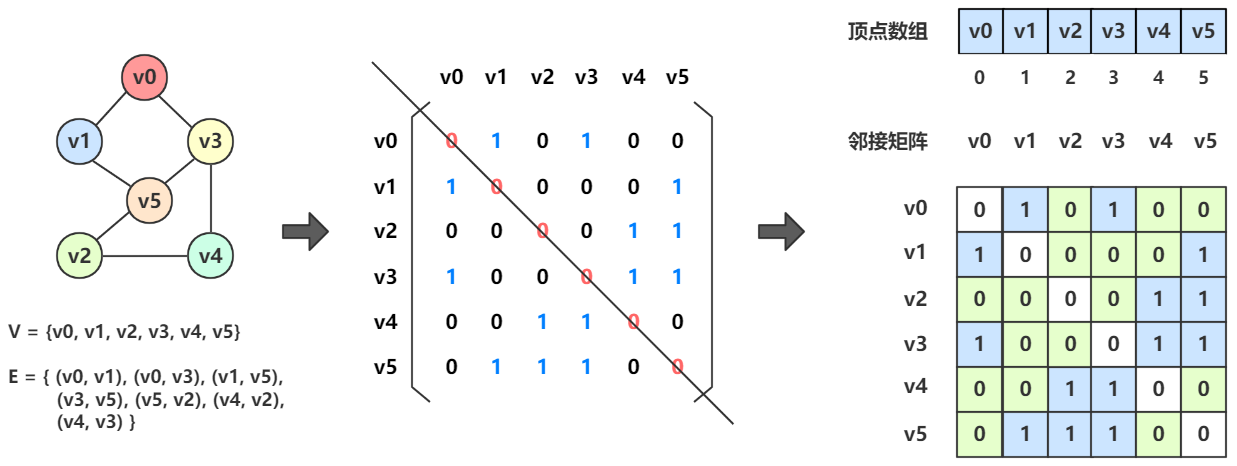
所以对于图 \(G =(V, {E})\)，可以使用一个一维数组来存储顶点集 \(V\)，再用一个二维数组来存储边集 \(E\)。 于是一张图可以变成下图所示：

上图中，有一个结构体 struct Graph，结构体中包含一个一维数组 Vertex[] 和一个二维数组 Edge[][]，一个 v_count 存储顶点数，一个 e_count 存储边数。

Vertex[] 用来存储顶点信息，Edge[][] 用来存储边的信息。

例如 \((v_1, v_2)\) 就将 Edge[0][1] 置为1；而 \((v_1, v_2)\) 也可以表示为 \((v_2, v_1)\) ，所以 Edge[1][0] 也应置为1。

而简单图不会有自己邻接自己的边，所以 Edge[0][0]、Edge[1][1]、Edge[2][2]、Edge[3][3] 均为0。

稍微观察可以发现，无向图的邻接矩阵一定是一个对称矩阵¹，于是我们可以很容易知道图中的信息：

1. 某个顶点的度，起始就是这个顶点 v_i 在邻接矩阵中第 i 行（或第 i 列）的元素之和。

   eg：顶点 \(v_3\) 的度就是 1+1+0+1 = 3

2. 求顶点 v_i 的所有邻接点就是在邻接矩阵中第 i 行所有元素为 1 的点。

   eg：顶点 \(v_2\) 的所有邻接点就遍历 Edge[1][...]，其中为 Eege[1][0]、Edge[1][2] 为1，表示 \(v_1\) 和 \(v_3\) 为邻接点。

代码实现

GraphModel.hMatrixGraph.hMatrixGraph.cmain.c

// GraphModel.h
#ifndef GRAPH_MODEL_H_INCLUDED
#define GRAPH_MODEL_H_INCLUDED

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX 4

typedef enum {
    ERROR,
    OK,
} Status;

typedef enum {
    DG,  // 有向图
    UDG, // 无向图
    DN,  // 有向网
    UDN, // 无向网
} GraphKind;

typedef char* Vertex; // 顶点数组类型
typedef int Edge;     // 邻接矩阵类型

#endif // GRAPH_MODEL_H_INCLUDED

// MatrixGraph.h
#ifndef MATRIX_GRAPH_H_INCLUDED
#define MATRIX_GRAPH_H_INCLUDED

#include "GraphModel.h"

typedef struct {
    Vertex vers[MAX];       // 顶点数组
    Edge   edges[MAX][MAX]; // 邻接矩阵（边数组）
    size_t v_count;         // 顶点总数
    size_t e_count;         // 边总数
    GraphKind kind;         // 图类型
} MatrixGraph;

/**
* @description: 创建无向图
* @param G 要操作初始化的图
* @return 成功返回OK，失败返回ERROR
*/
Status CreatUDG(MatrixGraph* G);

/**
* @description: 返回某个顶点在顶点集合中的下标
* @param G 要查找的图结构
* @param v 顶点
* @return 返回下标，不存在返回-1
*/
int LocateVex(MatrixGraph* G, Vertex v);

#endif // MATRIX_GRAPH_H_INCLUDED

// MatrixGraph.c
#include "MatrixGraph.h"

Status CreatUDG(MatrixGraph* G)
{
    G->kind = UDG;

    printf("Please type the count of Vertex : ");
    scanf("%d", &G->v_count);
    printf("Please type the count of Edge : ");
    scanf("%d", &G->e_count);

    // 录入顶点数组
    printf("Please type Vertex in turn.\n");
    for (int i = 0; i < G->v_count; i++) {
        G->vers[i] = calloc(10, sizeof(Vertex));
        printf("Vertex %d :", i);
        scanf("%s", G->vers[i]);
    }

    // 初始化邻接矩阵，所有边的权值设置为0
    for (int i = 0; i < G->v_count; i++) {
        for (int j = 0; j < G->v_count; j++) {
            G->edges[i][j] = 0;
        }
    }

    // 录入邻接矩阵
    printf("Please type Vertex and Adjacent. \n");
    for (int i = 0; i < G->e_count; i++) {
        Vertex v1 = calloc(10, sizeof(Vertex));
        Vertex v2 = calloc(10, sizeof(Vertex));

        printf("Vertex %d : ", i + 1);
        scanf("%s", v1);
        printf("Adjacent %d : ", i + 1);
        scanf("%s", v2);

        /** 核心代码 begin */

        // 获取顶点的下标
        int x = LocateVex(G, v1);
        int y = LocateVex(G, v2);
        if (x == -1 || y == -1)
            return ERROR;
        // 对应位置置为1
        G->edges[x][y] = 1;
        G->edges[y][x] = 1;

        /** 核心代码 end */

        free(v1);
        free(v2);
    }
    return OK;
}

int LocateVex(MatrixGraph* G, Vertex v)
{
    int index = 0;
    while (index < G->v_count) {
        if (strcmp(v, G->vers[index]) == 0) {
            break;
        }
        index++;
    }
    return index == G->v_count ? -1 : index;
}

void Test()
{
    MatrixGraph G;
    Status status = CreatUDG(&G);
    if (status = ERROR) {
        printf("Create Graph Failed~");
        return;
    }
    printf("The Adjacent Matrix: \n");
    printf("\t");
    for (int i = 0; i < G.v_count; i++) {
        printf("\t%s", G.vers[i]);
    }
    printf("\n");
    for (int i = 0; i < G.e_count; i++) {
        printf("\t%s", G.vers[i]);
        for (int j = 0; j < G.e_count; j++) {
            printf("\t%d", G.edges[i][j]);
        }
        printf("\n");
    }
}

#include "MatrixGraph.c"

int main(int argc, char const* argv[])
{
    Test();
    return 0;
}

有向图

理论描述

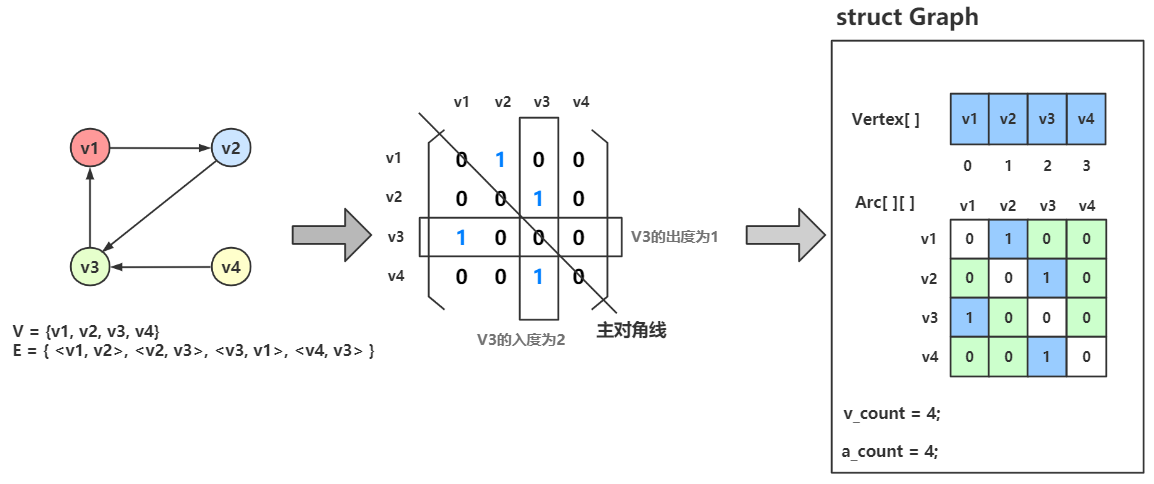
有向图和无向图的区别在于邻接矩阵。

在有向图邻接矩阵中，

• 第 \(i\) 行含义：以结点 \(v_i\) 为尾的弧（即出度边）
• 第 \(i\) 列含义：以结点 \(v_i\) 为头的弧（即入度边）

其特点为：

• 无向图的邻接矩阵一定是对称的，当有向图的邻接矩阵不一定是对称的。
• 顶点 \(v_i\) 的出度 = 第 \(i\) 行 元素之和
• 顶点 \(v_i\) 的入度 = 第 \(i\) 列 元素之和
• 顶点 \(v_i\) 的度 = 第 \(i\) 行元素之和 + 第 \(i\) 列元素之和

Note

口诀：

• Arc[行][列]
• Arc[出][入]
• 列头入，行尾出：即 列为弧头、入度；行为弧尾、出度。

代码实现

在代码实现上，有向图与无向图唯一的区别在于：录入弧的数据之后，只需要执行赋值一次就可以。

G->edges[x][y] = 1;
// G->edges[y][x] = 1;

这里我将有向图和无向图的创建合并在一起，在调用函数时多传入一个 GraphKind 类型参数来区分。

Status CreatGraph(MatrixGraph* G, GraphKind kind)
{
    G->kind = kind;
    // 录入顶点数和边数
    ...
    // 录入顶点数组
    ...
    // 初始化邻接矩阵，所有边的权值设置为0
    ...
    // 录入邻接矩阵
    printf("Please type %s and %s. \n", kind == UDG ? "Vertex" : "InDegree", kind == UDG ? "Adjacent" : "OutDegree");
    for (int i = 0; i < G->e_count; i++) {
        Vertex v1 = calloc(10, sizeof(Vertex));
        Vertex v2 = calloc(10, sizeof(Vertex));

        printf("%s %d : ", kind == UDG ? "Vertex" : "OutDegree", i + 1);
        scanf("%s", v1);
        printf("%s %d : ", kind == UDG ? "Adjacent" : "InDegree", i + 1);
        scanf("%s", v2);

        int x = LocateVex(G, v1);
        int y = LocateVex(G, v2);
        if (x == -1 || y == -1)
            return ERROR;

        G->edges[x][y] = 1;
        G->edges[y][x] = kind == UDG ? 1 : 0;    // 无向图置为1，有向图保持默认

        free(v1);
        free(v2);
    }
    return OK;
}

// Status status = CreatGraph(&G);
Status status = CreatGraph(&G, DG);

同时，有向图的顶点的度 = 出度 + 入度，可以实现一个函数根据图的类型来返回顶点的度。

/**
 * @description: 获取某个顶点的度
 * @param G 要查找的图
 * @param v 要查询度的顶点
 * @return 该顶点的度
 */
size_t GetDegree(MatrixGraph* G, Vertex v)
{
    // 获取无向图的度：累加第i行或第i列的元素之和
    // 获取有向图的度：累加第i行和第i列的元素之和并相加
    int index = LocateVex(G, v);
    int inDegree = 0;
    int outDegree = 0;
    for (int i = 0; i < G->e_count; i++) {
        inDegree += G->edges[i][index];
        outDegree += G->edges[index][i];
    }
    return G->kind == UDG ? inDegree : inDegree + outDegree;
}

无向图的度只需要返回行的和或列的和就行，有向图的度则需要相加再返回。

网

边或弧带权的图即为网。

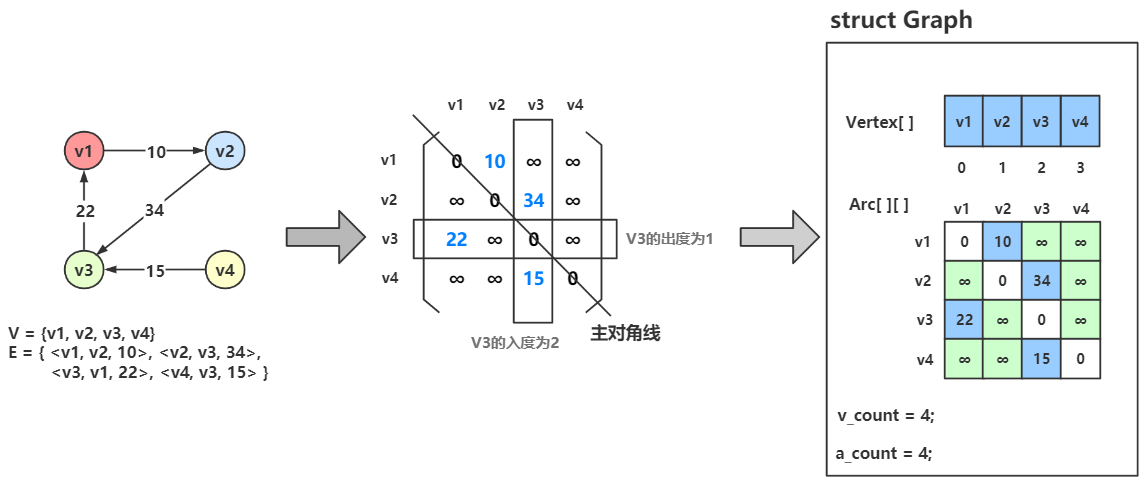
理论描述

设 图G 有 n 个顶点，则邻接矩阵是一个 \(n \times n\) 的方阵，定义为：

\[ Arc[i][j] = \begin{cases} W_{ij}, & {(v_i, v_j) \in E 或 \langle v_i, v_j \rangle \in E} \\\\ 0, & {i=j} \\\\ ∞, & {反之} \end{cases} \]

这里 \(W_{ij}\) 表示 \(\langle v_i, v_j \rangle\) 或 \((v_i, v_j)\) 上的权值。 \(\infty\) 表示一个计算机允许的、大于所有边上权值的值，即一个不可能的极限值，在C语言中可以使用 INT_MAX 来表示无穷。

代码实现

网的大部分代码与有向图和无向图的相同的，只有几处需要修改。

    // 初始化邻接矩阵，所有边的权值设置为无穷
    for (int i = 0; i < G->v_count; i++) {
        for (int j = 0; j < G->v_count; j++) {
            G->edges[i][j] = INT_MAX;
        }
    }

在初始化时，不能初始化为0，而要初始化为 INT_MAX。

// 录入邻接矩阵
    printf("Please type %s and %s. \n", kind == UDN ? "Vertex" : "InDegree", kind == UDN ? "Adjacent" : "OutDegree");
    for (int i = 0; i < G->e_count; i++) {
        Vertex v1 = calloc(10, sizeof(Vertex));
        Vertex v2 = calloc(10, sizeof(Vertex));
        int weight = 0; // 权值

        printf("%s %d : ", kind == UDN ? "Vertex" : "OutDegree", i + 1);
        scanf("%s", v1);
        printf("%s %d : ", kind == UDN ? "Adjacent" : "InDegree", i + 1);
        scanf("%s", v2);
        printf("Value %d: ", i + 1);
        scanf("%s", &weight);

        int x = LocateVex(G, v1);
        int y = LocateVex(G, v2);
        if (x == -1 || y == -1)
            return ERROR;

        G->edges[x][y] = weight;
        G->edges[y][x] = kind == UDN ? weight : INT_MAX;

        free(v1);
        free(v2);
    }

录入邻接矩阵时也需要多录入一个权值。

    // 邻接矩阵
    for (int i = 0; i < G.e_count; i++) {
        printf("\t%s", G.vers[i]);
        for (int j = 0; j < G.e_count; j++) {
            printf("\t%s", G.edges[i][j] == INT_MAX ? "∞" : (char*)G.edges[i][j]);
        }
        printf("\n");
    }

打印时也稍作处理。

邻接表 Adjacent List

邻接矩阵适合处理稠密图，对于稀疏图，邻接矩阵会造成巨大的浪费。在数据结构中，解决浪费问题需要往链式结构的方向去想。

Note

图的邻接表的存储方式是用一维数组和单链表来表示图。

一个一维数组用来存储图中的顶点集，多个单链表用来存储图中的边集。

图的邻接矩阵表示法 = 一维数组 \(\times\) 1 + 单链表 \(\times\) n

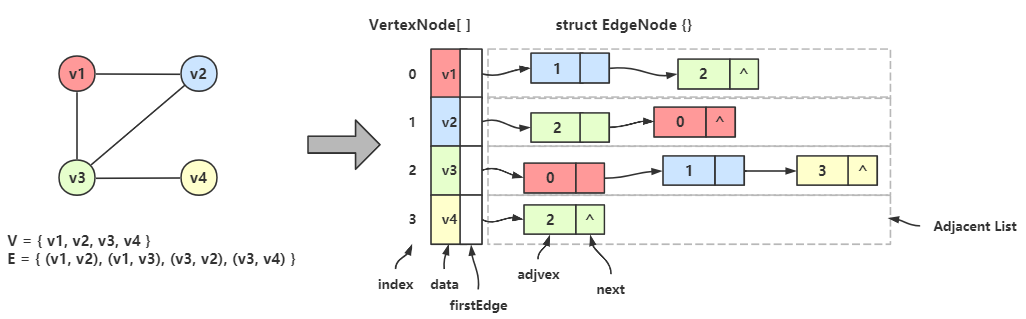
无向图的邻接表

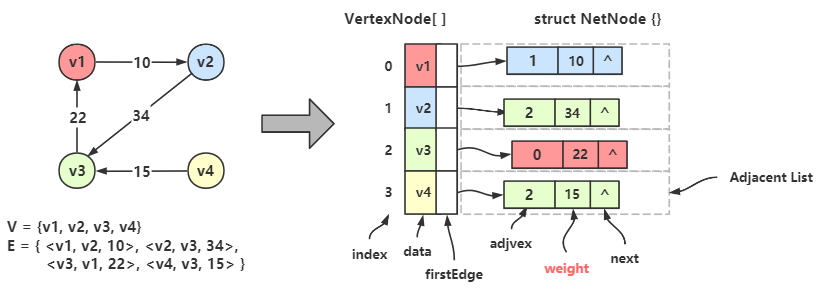
邻接表的处理方法如下：

• 图的顶点集用一维数组存储，数组元素为 数据域(data) + 首邻接点域(firstEdge)；
• 图的边/弧集用单链表存储，链表结点由 邻接点域(adjvex) + 指针域(next) 构成；

首邻接点域 指的是顶点的第一个边链表结点的地址，链表中的 邻接点域 存储的是邻接点的在顶点数组中的下标。

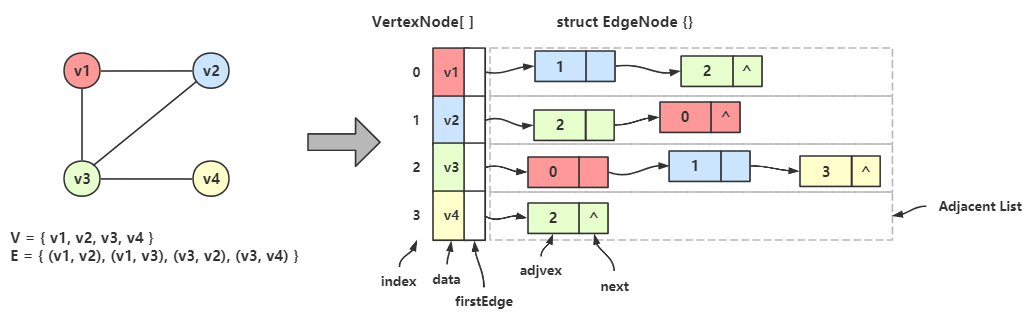
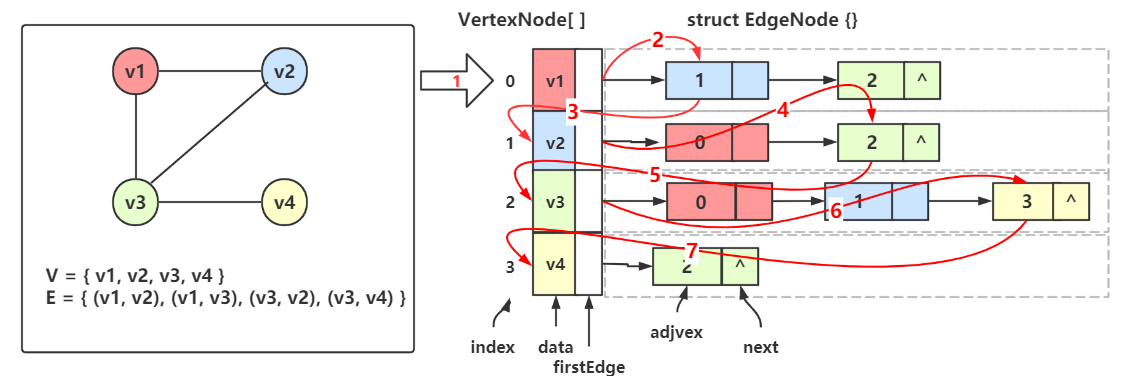
从上图可以看出，一个无向图可以用一个顶点类型的一维数组来存储顶点，每个顶点都各自有一条边链表，存储着该顶点的所有邻接点；

顶点数组中的某个顶点 Vertex[i] 和 对应边链表中的任一个结点构成了一条边。

eg：\(v_1\) 的邻接点是 \(v_2\) 和 \(v_3\)，在顶点数组中 \(v_1\) 的下标是 0；

在 Vertex[0] 数据域(data) 中存着 \(v_1\)，首邻接点域(firstEdge) 存储着边链的第一个结点的地址；

在边链的第一个结点中，邻接点域(adjvex) 存储着 \(v_2\) 的下标 1，然后指针域(next) 指向下一个结点；

下一个结点的邻接点域存储着 \(v_3\) 的下标 2，后面不再有了，所以指针域为空。

仔细观察可以发现以下特点：

• 无向图的邻接表重复存储着数据（邻接矩阵里也是），但总比邻接矩阵节省空间。
• 边链中的结点，除了与顶点数组中的元素，相互之间没有关系。
• 顶点的度 = 它的边链的结点数
• 求顶点的所有邻接点 = 遍历顶点的边链并取邻接点域
• 如果有 n 条边，则边链表会有 2n 个结点

有向图的邻接表

有向图的邻接表是类似的，但有向图区分方向。

• 我们以顶点为弧尾来存储边链表，并称这样的边链表为 出边表，或 正邻接表
• 我们以顶点为弧头来存储边链表，并称这样的边链表为 入边表，或 逆邻接表

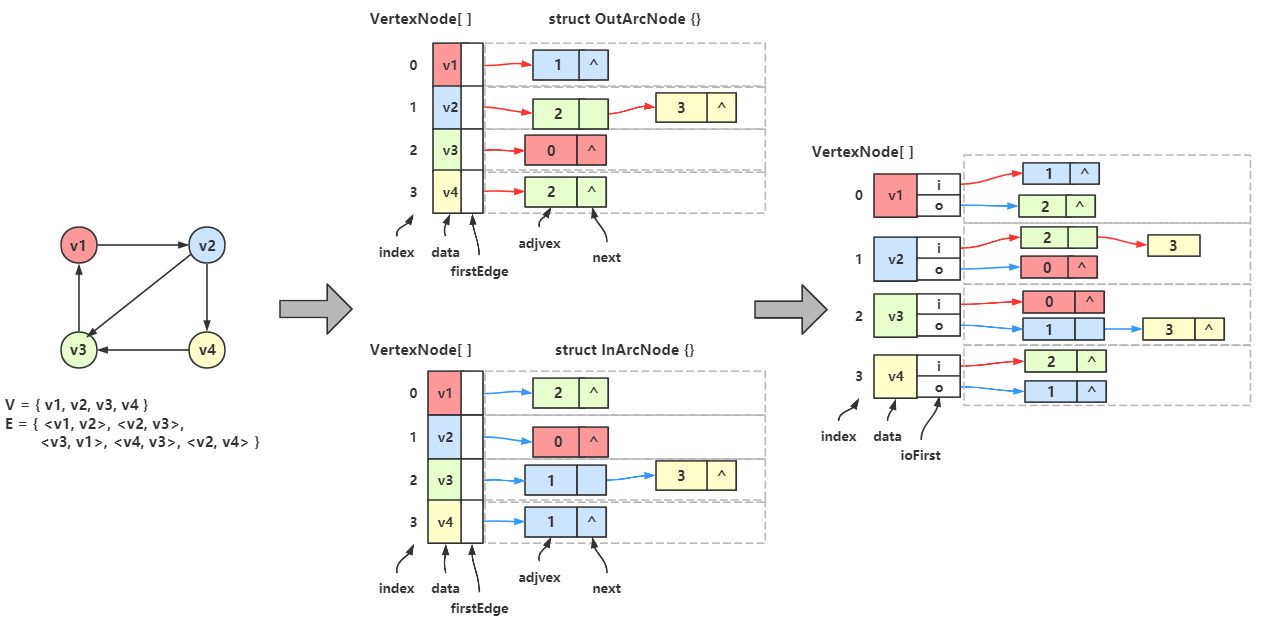
右上出边表 和 右下入边表

出边表中，顶点 \(v_1\) 作为弧尾，邻接弧头 \(v_2\)，所以首邻接点与指向出边表的第一个结点，结点中的数据域存储着弧头 \(v_2\) 的下标 1。所以 \(v_1\) 和 Vertex[1] 共同组成一条弧。

而顶点 \(v_2\) 有 2 个出度，所以 \(v_2\) 的出边表中有 2 个结点。

入边表中，顶点 \(v_3\) 作为弧头，邻接弧尾 \(v_2\) 和 \(v_4\)，所以首邻接点指向入边表的第一个结点，结点中存着 \(v_2\) 的下标 1，第二个结点存着 \(v_4\) 下标 3。

观察两个表，可以发现以下特点：

• 使用入边表表示图时，顶点的入度 = 对应入边表的结点数量，要计算出度只能遍历所有边链表
• 使用出边表表示图时，顶点的出度 = 对应出边表的结点数量，要计算入度只能遍历所有边链表
• 边链表中的结点，除了与顶点元素，相互之间没有关系
• 弧的总数 = 所有边链表的结点的总数之和

有向网的邻接表

有向网和无向网的邻接表仅仅只是在边链表中的结点增加一个变量 weight 来存储权值。同样有有向无向、出边入边之分。

代码实现

// 边链表结点类型
typedef struct node{
    int adjvex;          // 邻接点域、邻接点下标
    struct node* next;   // 指针域
} EdgeNode, ArcNode;

// 顶点类型
typedef char* Vertex;

// 顶点结点类型
typedef struct {
    Vertex data;         // 数据域
    EdgeNode firstEdge;  // 首邻接点域
} VertexNode;

// 图类型
typedef struct {
    VertexNode vexs[MAX];    // 顶点结点数组
    int v_count;             // 顶点数量
    int e_count;             // 边/弧数量
    GraphKind kind;          // 图类型
} AdjListGraph;

十字链表 Orthogonal List

Note

十字链表主要针对有向图，适用于需要 频繁获取顶点的入度和出度，频繁地判断一个点是不是另一个点 的邻接点等的情况。

其核心思想是**将出边表和入边表整合起来**。

有向图的邻接表只有表示出度的出边表，或者表示入度的入边表，鱼和熊掌不可兼得。

对于这种情况，小孩子才做选择，大人全都要！

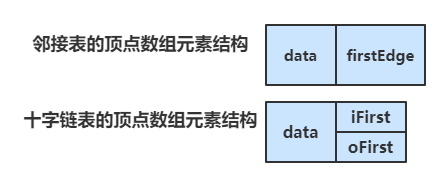
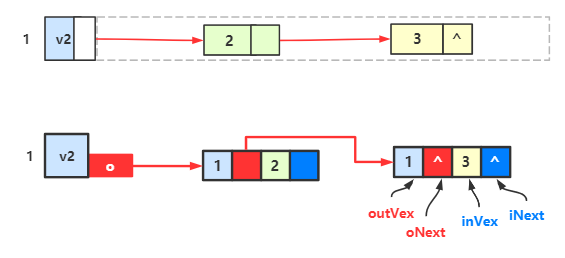
于是我们可以改造一下顶点数组，让一个顶点数组的元素包含 顶点、出边表的首邻接点域、入边表的首邻接点域

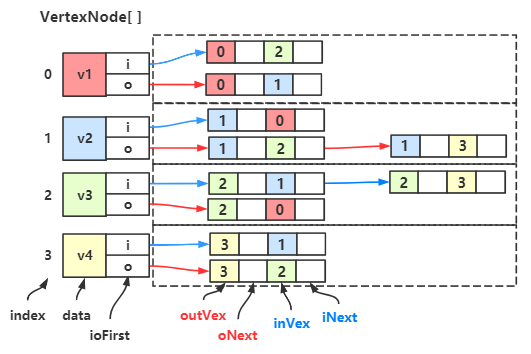
data 表示顶点，iFirst 表示入边表的首邻接点域，oFirst 表示出边表的首邻接点域。

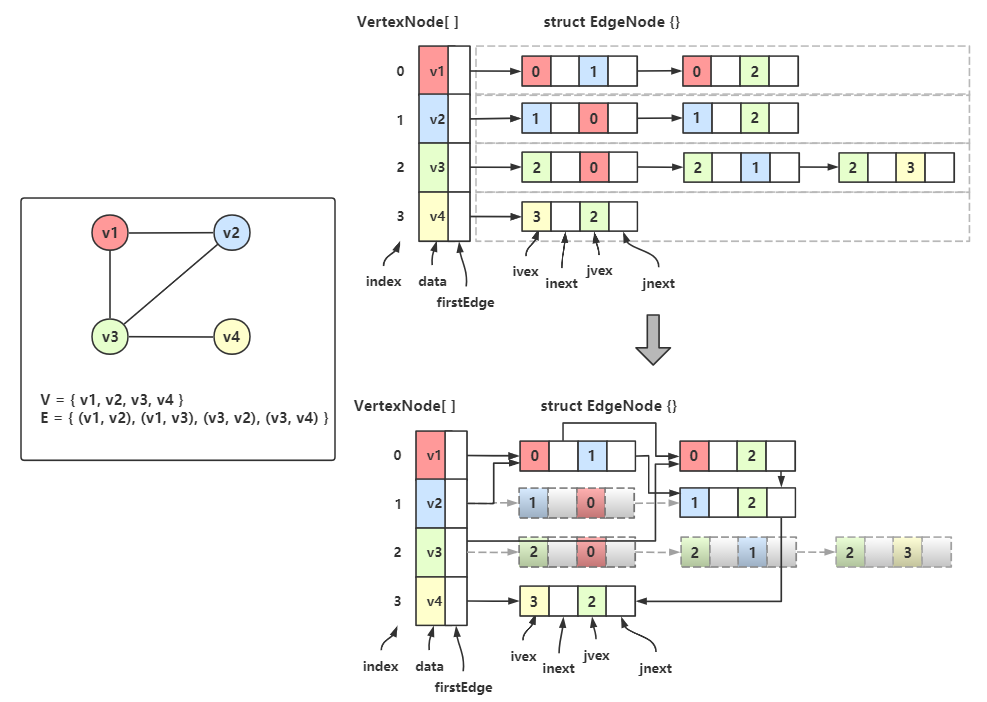
于是我们可以得到一个这样的双邻接表：

←图结构，↑出边表，↓入边表，→双邻接表

最左边是图结构，中间上面是出边表，中间下面是入边表，将它们结合，就成了最右边的双邻接表

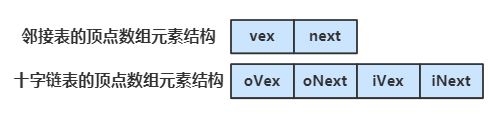
下一步我们改造一下边链表的结点，让它由 弧尾下标 + 弧尾边链的指针域 + 弧头下标 + 弧头边链的指针域 构成。

oVex 表示弧中出边的结点，即弧尾结点，的下标；oNext 替代了原出边表结点里的指针域；

iVex 表示弧中入边的结点，即弧头结点，的下标；iNext 替代了原入边表结点里的指针域；

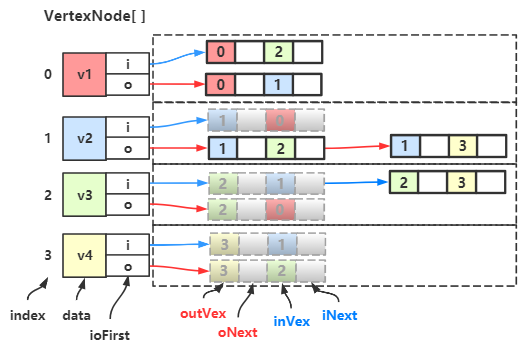
现在对双邻接表进行改造：

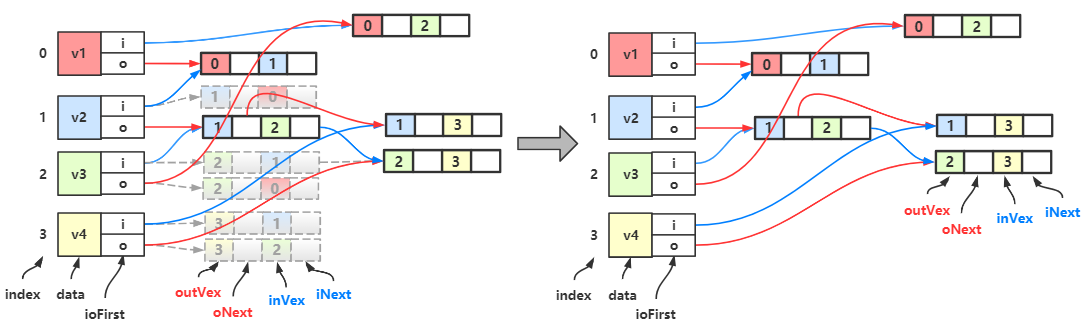
然后我们会发现有很多重复的结点，我们保留一个，删除一个：

接着把被删除的地方的链指向保留下来的那个结点：

例如 \(v_1\) 的出边表第一个结点（\(v_1\) 红色线条指向的那个 0 和 1 的结点） 和 \(v_2\) 的入边表的第一个节点（\(v_2\) 蓝色线条指向的那个 0 和 1 的结点），

这两个结点相同，

于是我删掉其中 \(v_2\) 的那个，然后让 \(v_2\) 的蓝色线指向 \(v_1\) 的第一个结点，其他结点也是同样操作。

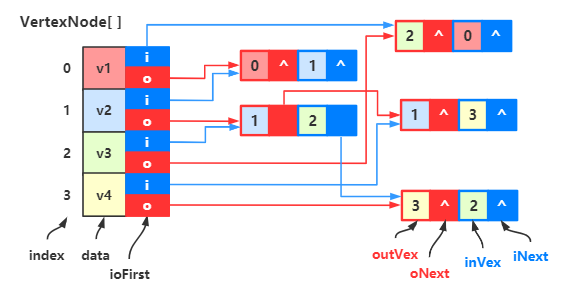
最后整理一下就是下图的样子：

对比一下该图的顶点 \(v_2\) 的出边表和十字链表：

可以看到没有损失任何信息。

代码实现

/** 顶点类型 */
typedef char* Vertex;

/** 十字链表结点 */
typedef struct node{
    Vertex oVex;        // 弧头下标
    Vertex iVex;        // 弧尾下标
    struct node* oNext; // 出边表指针域
    struct node* iNext; // 入边表指针域
    int weight;         // 权值
} OrthoNode;

/** 顶点数组元素类型 */
typedef struct {
    Vertex data;        // 顶点
    OrthoNode iFirst;   // 入边表的首个结点
    OrthoNode oFirst;   // 出边表的首个节点
} VertexNode;

/** 图结构 */
typedef struct {
    VertexNode vexArray[MAX];    // 顶点数组
    int v_count;                 // 顶点数量
    int a_count;                 // 弧的数量
    GraphKind kind;              // 图的类型（有向图/有向网）
} OrthoGraph;

总结

Note

十字链表5步走：

1. 生成有向图的出边表和入边表
2. 组合成双邻接表
3. 改造链表结点
4. 删除重复结点
5. 连接

邻接多重表 Adjacent Multilist List

邻接多重表主要是针对无向图。

从图中可以发现边链结点很多都是重复的。当删除一条边时，需要到两条边链中删除。 例如删除 边(\(v_1\), \(v_3\))，需要找到 \(v_1\) 的边链，删除第二个结点，然后还要找到 \(v_3\) 的边链，然后删除第一个结点。显然这是比较繁琐的。

所以邻接多重表就在邻接表的基础上对边链的结点进行改造。

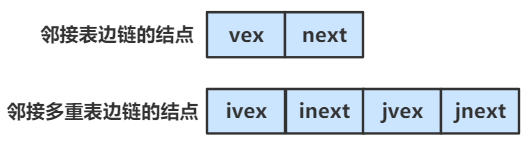
邻接表的结点由 邻接点的下标 + 下一结点指针 构成。

邻接多重表的结点由 顶点下标 + 顶点的下一结点的指针 + 邻接点下标 + 邻接点的下一结点的指针 构成。

其思想是 将所有顶点的边链整合起来，即节省空间，也提高了操作效率。

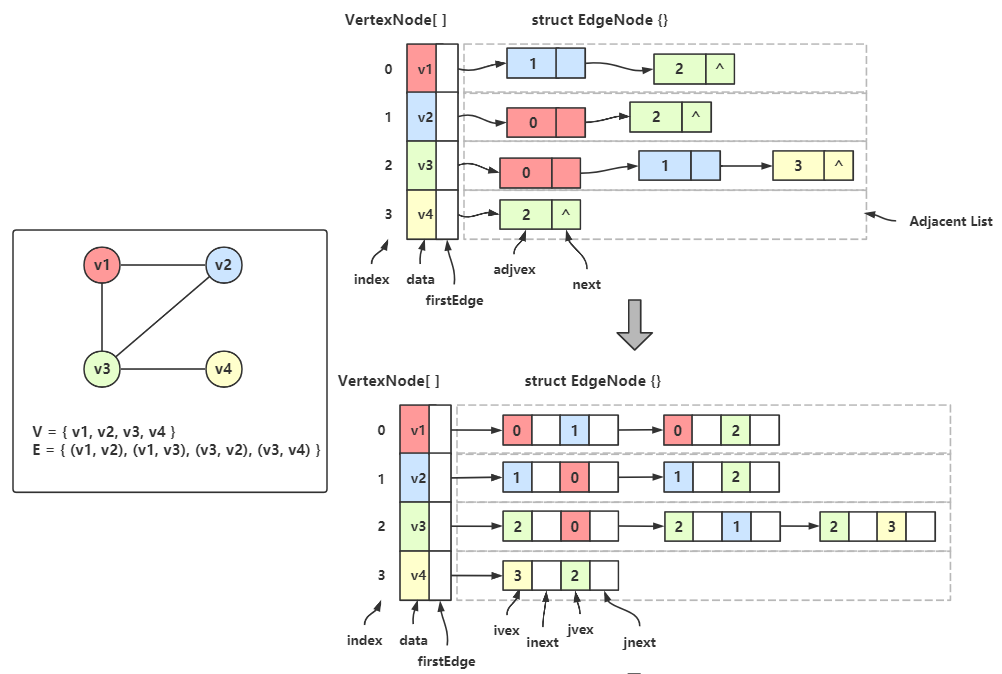
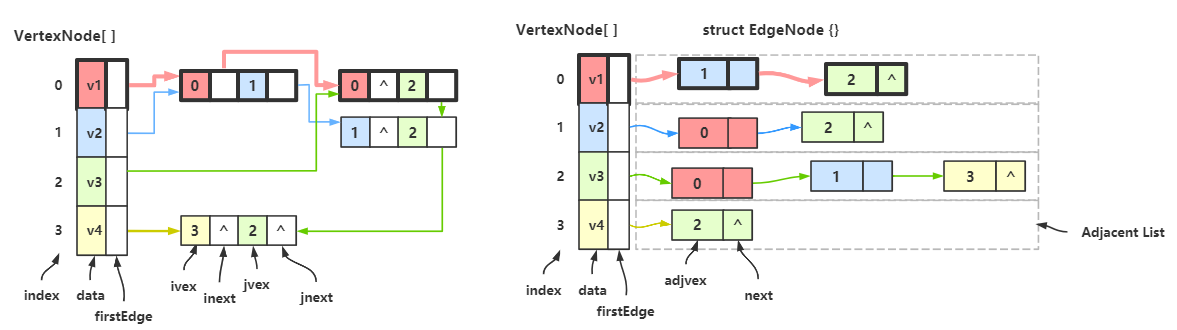
下面介绍一下如何将邻接表改为邻接多重表：

Step 1Step 2Step 3

首先将 边链的结点进行改造：边链结点中不仅要填入邻接点的下标，还要填入顶点自己的下标。

例如 顶点 \(v_1\) 有两个邻接点 \(v_2\) 和 \(v_3\)，所以要在两个结点中的 ivex 处填入 \(v_1\) 的下标 0。其他结点同理。看不懂可以对比两个图的边链。

例如 \(v_1\) 的第一个边链结点中有 0 和 1，代表 \(v_1\) 的地址和 \(v_2\) 的地址；\(v_2\) 的第一个边链结点也有 1 和 0，所以随便保留哪一个都可以。

图中将 \(v_2\) 的第一个边链结点删除，然后让 \(v_1\) 的第一个边链结点也成为 \(v_2\) 的边链结点。

这一步怎么删，删完指向谁可能有点乱，请看下面的图。

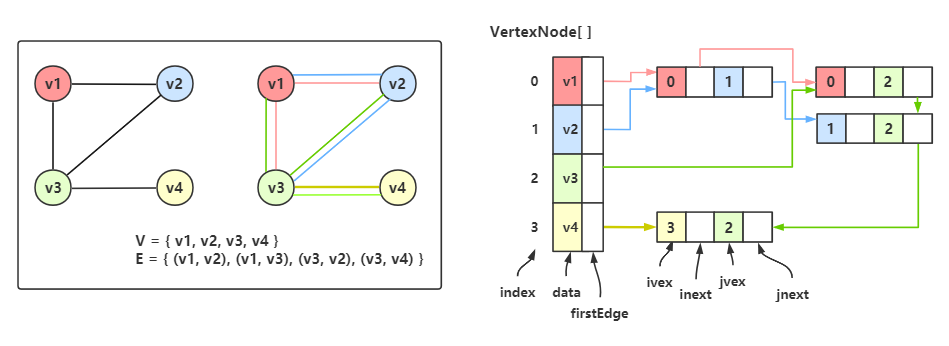
这里左侧两个图结构是同一个，第二个图结构多做了4条辅助线用来对照，实际真正的图是第一个的图结构，不要混淆。

对照第二个的图结构，和右侧的邻接多重表：

顶点 \(v_1\) 有两条边，邻接 \(v_2\) 和 \(v_3\)，在邻接多重表中用红色线连接起来了。单独观察 VertexNode[0] 和 红色线连接的两个结点，是不是跟邻接表相似？

同样道理可以继续观察 \(v_2\)、\(v_3\)、\(v_4\)。

我们会发现邻接多重表的结点数少了，而且 结点总数刚好就是边数。

现在再来体会那句：将所有边链整合起来，再体会体会为什么要增加 inext 和 jnext 两个元素在结点中，其实就是为了保留原本的信息。

邻接多重表中边链的结点不分是谁的，只记录边两头两个顶点的下标。

Tip

扩展一下，如果无向网使用邻接多重表表示，是不是只要将边链结点多加一个 权值 的成员即可？如果还要再来个是否被搜索过的标记，是不是再加个 布尔值 的成员即可？

边集数组 Edgeset Array

Note

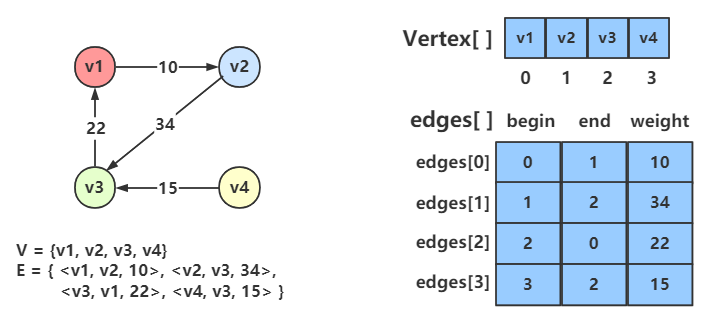
边集数组是由两个一维数组构成，一个是存储顶点的信息，另一个是存储边的信息。这个边数组的每个元素由一条边的起点下标 (begin) 、终点下标 (end) 和权 (weight) 组成。

边集数组关注的是边的集合。

在边集数组中要查找一个顶点的度需要扫描整个边数组，效率不高，因此更适合对边依次进行处理的操作，而不适合对顶点相关的操作。

适用情况总结

• 邻接矩阵适合处理稠密图
• 邻接表适合处理稀疏图
• 十字链表适合于需要频繁获取顶点的入度和出度，频繁地判断一个点是不是另一个点的邻接点等的情况
• 邻接多重表主要是针对无向图
• 边集数组适合对边依次进行处理的操作，而不适合对顶点相关的操作

图的遍历

深度优先搜索 DFS

深度优先遍历 (Depth-First-Search) 是仿树的前序遍历，该算法是利用栈来实现，也就是递归，所以在 DFS 中会有 递归 和 回溯 的说法。

DFS 需要借助一个数组来记录访问状态，这里将其称作 状态数组（Status Array）；该数组长度为顶点总数，次序与顶点数组相同。

从某一个顶点 \(v_i\) 出发，则当前顶点为 \(v_i\)；

先将该顶点标记为已访问，然后遍历其所有邻接点，找到 第一个未访问的邻接点 \(v_j\) 并置为当前顶点；

接着从该顶点 \(v_j\) 出发，先标记为已访问，然后遍历找到 第一个未访问的邻接点 vk 并置为当前顶点... 以此类推

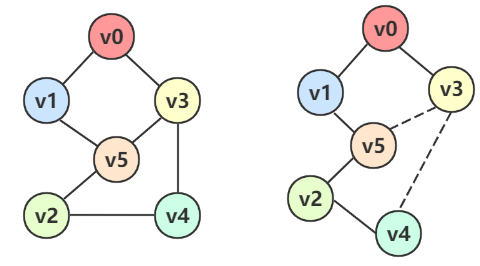
例如上图左边是一个图，我们可以转换一下思维，像右图一样把那两条边当作没有，就可以看成一棵二叉树

运用树的前序遍历法可以得到：** \(v_0\) -> \(v_1\) -> \(v_5\) -> \(v_2\) -> \(v_4\) -> \(v_3\) **，而这正好就是 DFS 的结果。

回过头来重新看着左边的图，假设从 v0 出发（其实图是无序的，从任何一点出发都可以）；

• \(v_0\) 有两个邻接点 \(v_1\) 和 \(v_3\)，我们先选择 \(v_1\)，然后从 \(v_1\) 出发；
• \(v_1\) 有两个邻接点 \(v_5\) 和 \(v_0\)，\(v_0\) 已经访问过了，只能选择 \(v_5\)，然后从 \(v_5\) 出发；
• \(v_5\) 有三个邻接点 \(v_1\)、\(v_2\)、\(v_3\)，\(v_1\) 已经访问过了，我们先选择 \(v_2\) ，然后从 \(v_2\) 出发；
• \(v_2\) 有两个邻接点 \(v_5\) 和 \(v_4\)，\(v_5\) 已经访问过了，只能选择 \(v_4\)，然后从 \(v_4\) 出发；
• \(v_4\) 有两个邻接点 \(v_2\) 和 \(v_3\)，\(v_2\) 已经访问过了，只能选择 \(v_3\)，然后从 \(v_3\) 出发；
• \(v_3\) 有三个邻接点 \(v_4\)、\(v_5\)、\(v_0\)，全都访问过了，到此遍历也就结束了。

如果仔细阅读上面6个步骤会发现，当我们遍历时，我们需要知道这个顶点是不是被访问过了，所以我们需要一个状态数组来记录；

而当有多个邻接点可以访问时，我们选择的依据，其实是顶点在顶点数组中存储的顺序所决定的。

例如在 \(v_5\) 的时候，选择了 \(v_2\) 而不是 \(v_3\)，其实是我们默认顶点数组是按照 v0、$v_1$、$v_2$、$v_3$、$v_4$、$v_5$ 的顺序存储，假设是按照 v0、$v_1$、$v_3$、$v_2$、$v_4$、$v_5$ 存储，\(v_3\) 在 \(v_2\) 前，则会先访问 \(v_3\)。

邻接矩阵的 DFS

先将图的边用矩阵表示，在计算机中使用二维数组存储。 然后设置一个状态数组，长度和顶点数组相同。

接下来就可以执行 DFS 了。

• 第一步：先初始化状态数组为未访问状态，即最开始所有顶点都未访问。
• 第二步：遍历顶点数组，让数组里每个顶点都放入遍历执行函数中，不过在调用遍历执行函数之前要先判断顶点是否已被访问。

int visited[MAX];

/** DFS begin */

/**
 * @description: 深度优先遍历算法
 * @param G 需要被遍历的图
 * @return 无
 */
void DFSTraverse_AMG(MatrixGraph* G)
{
    // 初始化状态数组
    for (int i = 0; i < G->v_count; i++)
        visited[i] = UNVISITED;
    // DFS 遍历
    for (int i = 0; i < G->v_count; i++)
        if (!visited[i]) // 如果某个顶点未访问
            DFS_AMG(G, i); // 调用遍历执行函数
}

遍历执行函数就是 DFS 的核心算法了。 该函数接收顶点的下标，并做3件事：

1. 访问当前顶点
2. 更改顶点的访问状态
3. 获取第一个未访问的邻接点下标，然后递归进去，找不到则回溯

/**
 * @description: 深度优先搜索的核心算法
 * @param G 要搜索的图
 * @param index 要搜索的顶点的下标
 * @return 无
 */
void DFS_AMG(MatrixGraph* G, int index)
{
    printf("-> %s ", G->vexes[index]); // 访问当前顶点
    visited[index] = VISITED; // 更改当前顶点的访问状态

    for (int j = 0; j < G->v_count; j++)
        if (G->matrix[index][j] && !visited[j]) // 获取第一个未访问的邻接点下标然后递归进去
            DFS_AMG(G, j);
}
/** DFS end */

在邻接矩阵中，获取某个顶点的所有邻接点就是遍历其所在的行，找到第一个未访问的邻接点。

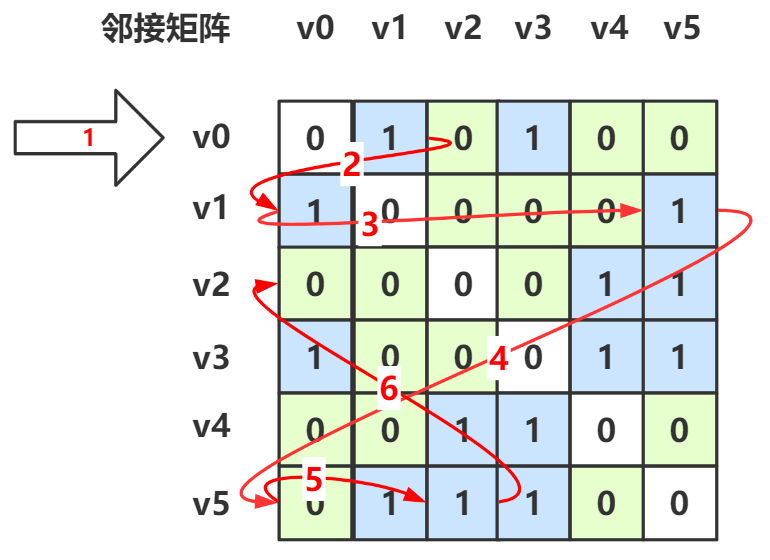
从邻接矩阵中看如上图

• 最开始从第 0 行进行（箭头1），找到第一个邻接点的下标，其列标为 1，于是跳到第 1 行（箭头2）
• 第 1 行第一个邻接点是 v0 ，已经访问过，所以跳过（箭头3），一直找到 \(v_5\) 这个邻接点，其列标为 5，于是跳到第 5 行（箭头4）
• 第 5 行第一个邻接点的 \(v_1\)，已经访问过，所以跳过（箭头5），接下去找到第二个邻接点 \(v_2\)，其列标为 2，于是跳到第 2 行（箭头6）
• 接下去的步骤都是这个思路，画出来太乱就没画了。

邻接表的 DFS

邻接表的具体代码实现跟邻接矩阵稍稍不同而已，只不过把数组处理换成了链表处理

• 最开始从 \(v_1\) 开始（箭头1），访问 \(v_1\) 的边链上第一个结点（箭头2），得到了 \(v_2\) 的下标，于是跳到 \(v_2\)（箭头3）
• 接着从 \(v_2\) 开始，先访问 \(v_2\)，然后遍历 \(v_2\) 的边链上的结点（箭头4），第一个结点 0 是 \(v_1\) 的下标，已经访问过了，于是继续下一个结点，得到了 \(v_3\) 的下标，于是跳到 \(v_3\)（箭头5）
• 接着从 \(v_3\) 开始，先访问 \(v_3\)，然后遍历 \(v_3\) 的边链上的结点（箭头6），第一和第二个结点是 \(v_1\) 和 \(v_2\) 的下标，已经访问过，所以接着下一个结点，得到 \(v_4\) 的下标，于是跳到 \(v_4\)（箭头7）
• 接着从 \(v_4\) 开始，先访问 \(v_4\)，然后遍历 \(v_4\) 的边链上的结点，发现得到的是 \(v_3\) 的下标，已经访问过了，再下去没有了，于是结束。

void DFSTraverse_ALG(AdjListGraph* G)
{
    //  初始化状态数组
    for (int i = 0; i < G->v_count; i++)
        visited[i] = UNVISITED;
    // DFS遍历
    for (int i = 0; i < G->v_count; i++)
        if (!visited[i]) // 如果顶点没有被访问，就递归调用
            DFS_ALG(G, i);
}

void DFS_ALG(AdjListGraph* G, int index)
{
    printf(" -> %s", G->vexes[index].data);    // 访问顶点
    visited[index] = VISITED;                  // 更改状态

   // 寻找邻接点
    EdgeNode* eNode = G->vexes[index].firstEdge;
    while (eNode) {
        if (!visited[eNode->adjvex]) // 如果邻接点未访问就递归访问
            DFS_ALG(G, eNode->adjvex);
        eNode = eNode->nextEdge;
    }
}

DFSTraverse_ALG() 和 DFSTraverse_AMG() 是一样的，初始化状态数组，然后遍历顶点数组，调用 DFS 算法

DFS_AMG() 中是遍历某一行，DFS_ALG() 中是遍历某一条链表，执行的逻辑都是如果邻接点为访问就递归。

时间复杂度

在遍历图时，对图中每个顶点至多调用一次 DFS 函数，因为一旦某个顶点被标志成已访问后，就不再从它出发进行搜索。 因此，深度遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费时间取决于所采用的存储结构。

• 当用邻接矩阵时，使用的是二位数组，查找每个顶点的邻接点所需时间为 \(O(n^2)\)，n 为图中顶点数。
• 当用邻接表时，使用的是链表，查找每个顶点的邻接点所需时间为 \(O(e)\)，e 为无向图中边的数量，或有向图中弧的数量。

由此， 邻接矩阵的 DFS 时间复杂度为 \(O(n^2 + n) = O(n^2)\) 邻接表的 DFS 时间复杂度为 \(O(n+e)\)

广度优先 BFS

广度优先遍历 (Breadth-First-Search) 是仿树的层次遍历。该算法是利用队列实现的。

BFS 的思想是，把顶点都放到队列中，当访问一个顶点，即为出队一个元素；当出队一个元素时，需将其所有未访问的邻接点入队。

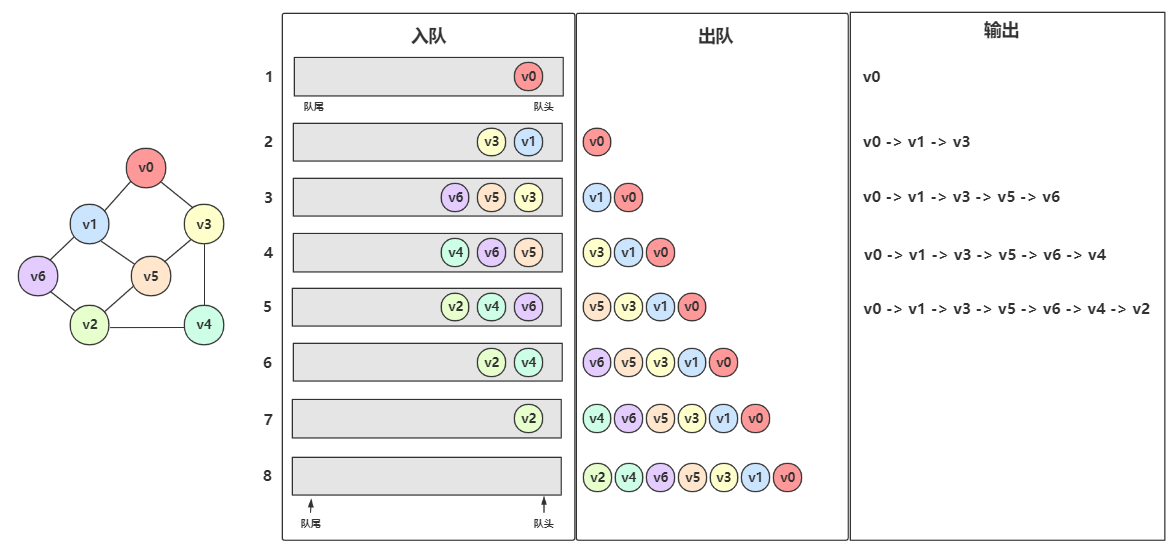
1. 先从 \(v_0\) 开始遍历，打印 \(v_0\)，然后 \(v_0\) 入队
2. 队列不为空，\(v_0\) 出队，同时 \(v_0\) 的未入队且未访问的邻接点 \(v_1\)、\(v_3\) 入队，然后访问 \(v_1\)、\(v_3\)
3. 队列不为空，\(v_1\) 出队，同时 \(v_1\) 的未入队且未访问的邻接点 \(v_5\)、\(v_6\) 入队，然后访问 \(v_5\)、\(v_6\)
4. 队列不为空，\(v_3\) 出队，同时 \(v_3\) 的未入队且未访问的邻接点 \(v_4\) 入队，然后访问 \(v_4\)
5. 队列不为空，\(v_5\) 出队，同时 \(v_5\) 的未入队且未访问的邻接点 \(v_2\) 入队，然后访问 \(v_2\)
6. 队列不为空，\(v_6\) 出队，同时 \(v_6\) 已经没有未入队且为访问的邻接点了，不做入队操作
7. 队列不为空，\(v_4\) 出队
8. 队列不为空，\(v_2\) 出队

队列为空，结束

到此 BFS 执行完毕

所以该图的 BFS 顺序为 \(v_0\) -> \(v_1\) -> \(v_3\) -> \(v_5\) -> \(v_6\) -> \(v_4\) -> \(v_2\)。

队列

BFS 需要借助队列实现，下面是队列的代码：

LinkQueue.hLinkQueue.c

// LinkQueue.h
#ifndef LINK_QUEUE_H_INCLUDED
#define LINK_QUEUE_H_INCLUDED
#include "GraphModel.h"

typedef Vertex Element;

// 结点
typedef struct QueueNode {
    Element data;
    struct QueueNode* next;
} QueueNode;

// 队列
typedef struct {
    QueueNode* front;
    QueueNode* rear;
} LinkedQueue;

Status InitLinkedQueue(LinkedQueue* q);
Status EnQueue(LinkedQueue* q, Element e);
Status DeQueue(LinkedQueue* q, Element* e);
bool isEmptyQueue(LinkedQueue* q);
void PrintLinkedQueue(LinkedQueue* q);

#endif // LINK_QUEUE_H_INCLUDED

// LinkQueue.c
#include "LinkQueue.h"

Status InitLinkedQueue(LinkedQueue* q)
{
    q->front = NULL;
    q->rear = NULL;
    return OK;
}

Status EnQueue(LinkedQueue* q, Element e)
{
    QueueNode* new = malloc(sizeof(QueueNode));
    new->data = e;
    new->next = NULL;

    if (isEmptyQueue(q)) { // 处理空队情况
        q->front = q->rear = new;
        return OK;
    } else { // 处理非空队情况
        q->rear->next = new; // 原队尾结点的next指向新结点
        q->rear = new; // 更新队尾指针
        return OK;
    }
    return ERROR;
}

Status DeQueue(LinkedQueue* q, Element* e)
{
    if (isEmptyQueue(q)) { // 空队直接返回
        e = NULL;
        return OK;
    }

    if (q->front == q->rear) { // 处理队中只有一个结点的情况
        *e = q->front->data;
        free(q->front);
        q->front = q->rear = NULL;
        return OK;
    }
    // 处理队中不止一个结点的情况
    QueueNode* del = q->front; // 标记队头结点
    q->front = del->next; // 队头指针指向下一个结点
    *e = del->data; // 取数据
    free(del); // 删除原队头结点
    del = NULL;
    return OK;
}

bool isEmptyQueue(LinkedQueue* q)
{
    return q->front == NULL || q->rear == NULL;
}

void PrintLinkedQueue(LinkedQueue* q)
{
    if (isEmptyQueue(q)) {
        printf("Queue Empty");
    }

    QueueNode* p = q->front;
    while (p) {
        printf("\t%s ", p->data);
        p = p->next;
    }
}

邻接矩阵的 BFS

/** BFS begin */
void BFSTraverse_AMG(MatrixGraph* G)
{
    for (int i = 0; i < G->v_count; i++)
        visited[i] = UNVISITED;

    // 循环遍历每个顶点
    for (int i = 0; i < G->v_count; i++)
        if (!visited[i]) // 如果没有访问过就遍历访问
            BFS_AMG(G, i);
}

void BFS_AMG(MatrixGraph* G, int index)
{
    printf("-> %s ", G->vexes[index]);    // 访问顶点
    visited[index] = VISITED;             // 更改访问状态

    LinkQueue queue;
    InitLinkedQueue(&queue);            // 初始化队列
    EnQueue(&queue, G->vexes[index]);   // 当前顶点入队，对应上图中第一步的 v0 入队
    while (!isEmptyQueue(&queue)) {    // 取出队头元素，遍历队头顶点的所有邻接点

        Vertex vex;
        DeQueue(&queue, &vex);     // 取出的队头顶点
        // 获取该顶点的所有邻接点
        for (int i = FirstAdjVex_AMG(G, vex); i; i = SecondAdjVex_AMG(G, vex, G->vexes[i])) {
            if (!visited[i]) {
                printf("-> %s ", G->vexes[i]);    // 遇到顶点的邻接点先访问
                visited[i] = VISITED;
                EnQueue(&queue, G->vexes[i]);     // 再入队
            }
        }

    }
}

int FirstAdjVex_AMG(MatrixGraph* G, Vertex v)
{
    int defaultWeight = G->kind <= 1 ? 0 : INT_MAX; // 图/网 的默认权重

    int vex_index = LocateVex(G, v); // 获取顶点下标
    if (vex_index == -1)
        return ERROR;

    // 搜索图的邻接矩阵中域顶点v的第一个邻接点下标
    for (int j = 0; j < G->v_count; j++)
        if (G->matrix[vex_index][j] != defaultWeight)
            return j;

    return 0;
}

int SecondAdjVex_AMG(MatrixGraph* G, Vertex v1, Vertex v2)
{
    int defaultWeight = G->kind <= 1 ? 0 : INT_MAX; // 图/网 的默认权重
    int index1 = LocateVex(G, v1);
    int index2 = LocateVex(G, v2);
    if (index1 == -1 || index2 == -1)
        return 0;

    for (int i = index2 + 1; i < G->v_count; i++)
        if (G->matrix[index1][i] != defaultWeight)
            return i;

    return 0;
}
/** BFS end */

邻接表的 BFS

按理来说邻接矩阵的 BFS 和邻接表的 BFS 应该是一样的，至少在无向图中是一样的。 但是如果邻接表是用的头插法，那可能结果是不一样的

void BFSTraverse_ALG(AdjListGraph* G)
{
    for (int i = 0; i < G->v_count; i++)    // 初始化状态数组
        visited[i] = UNVISITED;

    for (int i = 0; i < G->v_count; i++)    // 遍历顶点数组，逐一对每一个未访问的顶点执行 BFS
        if (!visited[i])
            BFS_ALG(G, i);
}

void BFS_ALG(AdjListGraph* G, int index)
{
    printf("-> %s ", G->vexes[index].data);    // 访问顶点
    visited[index] = VISITED;                  // 更改顶点状态

    LinkQueue queue;
    InitLinkedQueue(&queue);
    EnQueue(&queue, G->vexes[index].data);     // 当前顶点入队

    while (!isEmptyQueue(&queue)) {    // 取出队头元素，遍历队头顶点的所有邻接点
        Vertex vex;
        DeQueue(&queue, &vex);    // 取出队头元素
        // 遍历所有邻接点
        EdgeNode* node = G->vexes[LocateVex_ADJ(G, vex)].firstEdge;
        while (node) {
            if (!visited[node->adjvex]) {
                printf("-> %s ", G->vexes[node->adjvex].data);    // 邻接点先访问
                visited[node->adjvex] = VISITED;
                EnQueue(&queue, G->vexes[node->adjvex].data);    // 再入队
            }
            node = node->nextEdge;
        }
    }
}

时间复杂度

在遍历图时，每个顶点最多进一次队列，遍历图的过程实质上是通过边或弧找邻接点的过程。 因此，广度优先搜索、深度优先搜索，在遍历图时的时间复杂度是相同的。

总结

1. 存储结构：

   • 邻接矩阵：一维数组存储顶点集+二维数组存储边/弧
   • 邻接表：一维数组存储顶点集+单链表存储边/弧
     • 出边表：链表的结点存储的是弧头的下标
     • 入边表：链表的结点存储的是弧尾的下标
   • 十字链表：将出边表和入边表整合起来，主要针对有向图
   • 邻接多重表：将所有边链的结点整合起来，去除重复的结点，主要针对无向图
   • 边集数组：一维数组存储顶点集+一维数组存储边集，关注的是边

2. 图的遍历：

   • 深度优先搜索 DFS 和 广度优先搜索 BFS 是图的最基本的遍历方式。
   • DFS 是仿树的前序遍历，利用栈做辅助，具体实现是不断将当前顶点的第一个未访问邻接点拿去递归。
   • BFS 是仿树的层序遍历，利用队列做辅助，具体实现是每当出队一个元素时，就访问其所有未访问且未入队的邻接点，并将这些邻接点入队。
   • 使用邻接矩阵存储和使用邻接表存储的图在做 DFS 或 BFS 时没什么区别，只不过邻接矩阵是操作二维数组，邻接表是操作链表。

---

1. 对称矩阵：n 阶矩阵的元满足 \(a_{ij} = a_{ji}, (0 \leq i, j \leq n)\)，即从矩阵左上角到右下角的主对角线为轴，右上角的元与左下角相对应的元完全相等。 ↩